查看高亮文档请点击:
[https://www.zybuluo.com/huangyichun/note/739561]
定义:二叉查找树是一棵二叉树,且每个节点的值都大于左子树的值,小于右子树的值。
如下图所示:
**
其中数字代表二叉查找树的键,字母代表二叉查找树的值**
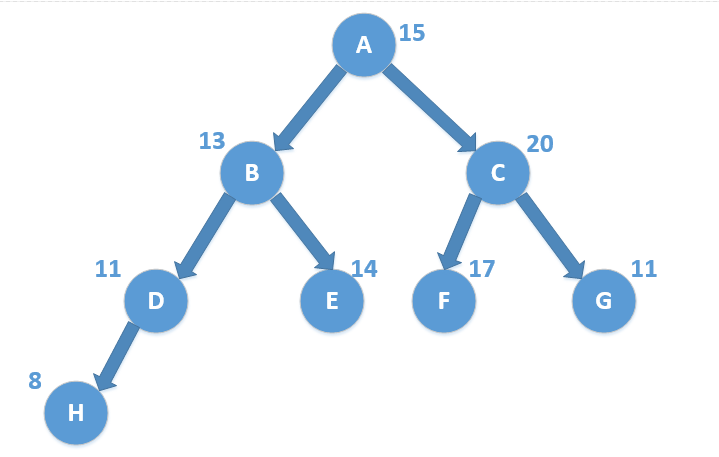
image.png-46.7kB
我们可以通过二叉树的中序遍历二叉查找树得到一个有序的数组。
数据表示:设计一个二叉查找树类,在类中嵌套一个私有类表示二叉查找树的一个节点,每个节点都有一个键和一个值,一个左链接和一个右链接,和一个节点计数器。左链接指向一棵小于该节点的二叉排序树,右链接指向一棵大于该节点的二叉排序树。
/**
* 二叉查找树实现
*/
public class BST <Key extends Comparable<Key>, Value> {
private Node root; //根节点
private class Node{
private Key key; //键
private Value val; //值
private Node left, right; //左右子树的链接
private int N; //以该节点为根的子树中的节点总数
public Node(Key key, Value val, int N) {
this.key = key;
this.val = val;
this.N = N;
}
}
public void printfBST(){
printfBST(root);
}
/**
* 中序打印二叉查找树
* @param node
*/
private void printfBST(Node node){
if(node == null)
return;
printfBST(node.left);
System.out.print(node.key+" ");
printfBST(node.right);
}
/**
* 从根节点出发,查找树中排名为K的键,即正好有k个小于它的键
* @param k
* @return
*/
public Key select(int k){
return select(root, k).key;
}
/**
* 删除最小键值的节点
*/
public void deleteMin(){
root = deleteMin(root);
}
/**
* 删除键值为key的节点
* @param key
*/
public void delete(Key key){
root = delete(root,key);
}
/**
* 以Node为根节点删除某个键为key的节点
* 1.首先找到值为Key的节点
* 2.如果node没有右子树,返回node的左子树,
* 如果node没有左子树,返回node的右子树
* 3.如果node左右子树都存在,则在node的右子树中找到最小的一个
* 节点,替代node
* @param node
* @param key
* @return
*/
private Node delete(Node node , Key key){
if(node == null)
return null;
int cmp = key.compareTo(node.key);
if(cmp < 0)
node.left = delete(node.left, key);
else if(cmp > 0)
node.right = delete(node.right, key);
else {
if(node.right == null) return node.left;
if(node.left == null) return node.right;
Node t = node;
node = min(node.right);
node.right = deleteMin(t.right);
node.left = t.left;
}
node.N = size(node.left) + size(node.right) + 1;
return node;
}
/**
* 以node为根节点删除最小的节点
* @param node
* @return
*/
private Node deleteMin(Node node){
if(node.left == null)
return node.right;
node.left = deleteMin(node.left); //删除最小节点
node.N = size(node.left) + size(node.right) + 1;//更新节点数
return node;
}
/**
* 从Node节点出发,查找树中排名为K的键,即正好有k个小于它的键
* @param node
* @param k
* @return
*/
private Node select(Node node, int k){
if(node == null)
return null;
int t = size(node.left);//左子树个数
if(t > k) return select(node.left,k);
else if(t < k) return select(node.right, k-t-1);//右子树中查找
else return node;
}
/**
* 从根节点开始查找Key
* 如果存在返回,不存在找到第一个小于该key的键
* @param key
* @return
*/
public Key floor(Key key){
Node node = floor(root, key);
if(node == null) return null;
return node.key;
}
/**
* 从node节点开始查找Key
* 如果存在返回,不存在找到第一个小于该key的键
* 即向下取整
* @param node
* @param key
* @return
*/
private Node floor(Node node, Key key){
if(node == null)
return null;
int cmp = key.compareTo(node.key);
if(cmp == 0) return node;
else if(cmp < 0) return floor(node.left, key);
Node t = floor(node.right, key);//查找右子树中是否有小于Key的节点
if(t != null) return t;
else return node;
}
/**
* 查找根节点最大的键
* @return
*/
public Key max(){
return max(root).key;
}
/**
*查找以node节点为根节点的最大键
* 如果左子树为空,则当前节点为最大值
* 否则最小值就是左子树的最大值
* @param node
* @return
*/
private Node max(Node node){
if(node.right == null)
return node;
return max(node.right);
}
/**
* 查找根节点最小的键
* @return
*/
public Key min(){
return min(root).key;
}
/**
* 查找以node节点为根节点的最小键
* 如果左子树为空,则当前节点为最小值
* 否则最小值就是左子树的最小值
* @param node
* @return
*/
private Node min(Node node){
if(node.left == null) return node;
return min(node.left);
}
/**
* 查找key存在则修改更新它的值,否则创建一个新的节点
* @param key
* @param value
*/
public void put(Key key, Value value){
root = put(root, key, value);
}
/**
* 如果Key存在于以node为根节点的子树中,则更新它的值
* 否则将以key和Value为键值对的新节点插入到该子树中
* @param node
* @param key
* @param value
* @return
*/
private Node put(Node node, Key key, Value value){
if(node == null)
return new Node(key, value, 1);
int cmp = key.compareTo(node.key);
if(cmp < 0) node.left = put(node.left, key, value);
else if(cmp > 0) node.right = put(node.right, key, value);
else node.val = value;
node.N = size(node.left) + size(node.right) + 1;//更新节点数
return node;
}
/**
* 获取Key对应的Value
* @param key
* @return
*/
public Value get(Key key){
return get(root, key);
}
/**
* 在以node为根节点的子树中查找并返回Key所对应的值
* @param node
* @param key
* @return
*/
private Value get(Node node, Key key){
if(node == null)
return null;
int cmp = key.compareTo(node.key);
if(cmp < 0) return get(node.left, key);
else if(cmp > 0) return get(node.right, key);
else return node.val;
}
/**
* 获取二叉查找树节点个数
* 满足 size(x) = size(x.left) + size(x.right) + 1;
* 对于空链接size(x)返回0
* @return 返回节点个数
*/
public int size(){
return size(root);
}
private int size(Node node){
if(node == null)
return 0;
else
return node.N;
}
}
构建上图的二叉查找树,对于里面的方法进行测试:
/**
* Created by huangyichun on 2017/5/1.
*/
public class Test {
public static void main(String[] args) {
BST<Integer,Character> bst = new BST<Integer, Character>();
bst.put(15,'A');
bst.put(13,'B');
bst.put(11,'D');
bst.put(8,'H');
bst.put(14,'E');
bst.put(20,'C');
bst.put(17,'F');
bst.put(11,'G');
bst.printfBST();
System.out.println();
System.out.println("最大键:" + bst.max());//打印最大键
System.out.println("最小键:" + bst.min());//打印最小键
System.out.println("Key= 15, value=" + bst.get(15));
System.out.println("节点个数为:" + bst.size());
bst.delete(13);//删除13这个节点
bst.printfBST();
// bst.deleteMin();
// bst.printfBST();
}
}
输出结果为:
8 11 13 14 15 17 20
最大键:20
最小键:8
Key= 15, value=A
节点个数为:7
8 11 14 15 17 20