角动量和磁矩

1.电子的磁矩

玻尔磁子

电子因轨道运动而具有磁矩:

$\mu = I S = - \frac{e}{T} \pi r^2$

$T = \frac{2\pi}{\omega}$

$\mu = - \frac{e}{2 \pi} \omega \pi r^2 = - \frac{e}{2m} mr^2 \omega$

考虑到:

$L = r \times p = mr^2 \omega$

$\mu = - \frac{e}{2m} L$

改写为:

$\vec \mu = - g \frac{e}{2m} \vec J$

这里引入了因子（朗德因子） $g$ ,

对轨道运动而言，

$g_L = 1$

因为电子还具有自旋运动, 自旋也会导致电子具有磁矩,

$g_S = 2$

回到电子的轨道磁矩,

$\vec \mu_L = - g_L \frac{e}{2m} \vec L$

角动量 $L$ 在 $z$ 方向的投影 $L_z$ ,

$L_z = m \hbar, m = 0, \pm 1, ... , \pm l$

$\vec \mu_L$ 在 $z$ 方向上的取值为,

$-\frac{e}{2m_e} m \hbar = - m \frac{e \hbar}{2 m_e} = - m \mu_B$

这里 $\mu_B$ 是玻尔磁子（Bohr magneton）, 即磁矩也是量子化的, 对电子而言, 其最小单位是玻尔磁子,

$\mu_B = \frac{e \hbar}{2 m_e} = 9.27400968(20) \times 10^{-24} \text{J} \cdot \text{T}^{-1}$

类似地，还可以定义核磁子（Nuclear magneton）

$\mu_N = \frac{e \hbar}{2 m_p} = 5.05078353(11) \times 10^{-27} \text{J} \cdot \text{T}^{-1}$

拉莫频率

Direction of precession for a negatively-charged particle. The large arrow indicates the external magnetic field, the small arrow the spin angular momentum of the particle.

磁矩 $\mu$ , 在磁场 $B$ 中, 能量是：

$U = - B \cdot \mu = - B \mu \cos \theta$

磁矩 $\mu$ 在磁场中的力矩 $\tau$ ,

$\tau = \mu \times B = \frac{d J}{ dt }$

利用

$\mu = - g \frac{e}{2m_e} J$

$- g \frac{e}{2m_e} \frac{d J }{d t} = \frac{d \mu}{dt} = - g \frac{e}{2m_e} \mu \times B = \omega \times \mu$

i.e.,

$g \frac{e }{2 m_e} B \times \mu = \omega \times \mu$

解出:

$\omega = g \frac{e}{2 m_e} B = g \frac{ \mu_B B}{\hbar}$

对轨道运动而言, $g_L =1$ ,

$\omega_L = \frac{\mu_B B}{\hbar}$

$\omega_L$ 是电子做轨道运动时的进动频率, 也叫拉莫频率(Larmor frequency)。

更一般地，可写为:

$\omega = g \omega_L$

比如，对自旋运动,

$\omega_S = 2 \omega_L$

旋磁比

回到公式,

$\vec \mu = - g \frac{e}{2m} \vec J$

可改写为,

$\vec \mu = \gamma \vec J$

这里的因子 $\gamma$ 叫旋磁比(Gyromagnetic ratio),

$\gamma = \frac{\mu}{J} = - g \frac{e}{2m} = - g \frac{\mu_B}{\hbar}$

对电子而言, 自旋朗德因子, 使用量子电动力学计算:

$g_S = 2\left( 1 + \frac{\alpha}{2 \pi} + ... \right)$

$\alpha = \frac{1}{137}$

得到,

$g_S = 2.00231930436153$

斯特恩-盖拉赫实验

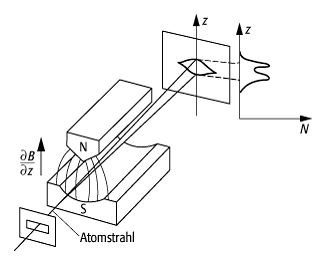
s2586_stern-gerlach-experiment.gif-10.5kB

斯特恩-盖拉赫实验示意

已知炉温600K，非均匀磁场强度 $\frac{\partial B_z}{\partial z} = 10^3 T \cdot m^{-1}$ , 磁铁长度 $L = 0.1 m$ , 磁铁到屏的距离是 $1m$ , 估算银原子在屏上的分裂 $P_2 P_3$ 。

首先估算银原子的速度,

$K = \frac{M v^2}{2} = \frac{3 k_B T}{2}$

$v = \sqrt{\frac{3 k_B T}{M} }$

银原子质量数 $107.9$ ,

$M = 107.9 u = 107.9 \times 931.494 \text{MeV} \cdot c^{-2}$

$k_B = 8.617 \times 10^{-5 } eV \cdot K^{-1}$

$3 k_B T = 3 \times 8.617 \times 10^{-5 } eV \cdot K^{-1} \times 600 K$

$3 k_B T = 0.155 eV$

$v = \sqrt{ \frac{ 0.155 }{10^{11} } } c = \sqrt{\frac{1.55 }{10^{12} }} c$

$v = \frac{1.245}{ 10^6} \times 3 \times 10^8 m \cdot s^{-1} = 374 m\cdot s^{-1}$

银原子飞跃磁铁的时间:

$\Delta t = \frac{0.1}{374} = 2.67 \times 10^{-4} s$

银原子磁矩,

$\mu = - 2 \frac{e}{2m_e} S$

磁矩在 $z$ 轴的投影,

$\mu_z = -2 \mu_B m_S$

这里 $m_S = \pm \frac{1}{2}$ ,

$\mu_z = \mp \mu_B$

在非均匀磁场中的受力，

$F_z = - \frac{\partial U_m}{\partial z} = \frac{ \partial \left( \mu_z B_z \right) }{\partial z} = \mp \mu_B \frac{\partial B_z}{\partial z}$

银原子在垂直方向的加速度,

$a = \frac{F_z}{M} = \mp \frac{ 9.274 \times 10^{-24} J \cdot T^{-1} \times 10^3 T \cdot m^{-1} }{107.9 \times 1.66 \times 10^{-27} kg } = \frac{9.274 \times 10^{-21} }{1.79 \times 10^{-25 } } = 5.18 \times 10^4 m \cdot s^{-2}$

在垂直方向获得的速度，

$\Delta v = a \Delta t = 5.18 \times 10^4 \times 2.67 \times 10^{-4} = 13.83 m \cdot s^{-1}$

张角,

$\Delta \theta = \frac{\Delta v }{v}=\frac{13.83}{374}$

银原子偏转,

$\Delta = \tan \theta \times 1 = 0.037 m$

考虑到银原子对称地向上、向下偏转，条纹间距为:

$2 \Delta = 0.074 m$

2.角动量相加和朗德因子

由于电子自旋运动朗德因子 $g_S=2$ 和电子轨道运动朗德因子 $g_L = 1$ 不同, 导致电子总角动量 $J$ 和电子总磁矩 $\mu$ 不共线。

$J = L + S$

这个求和首先是向量求和，其次它们都是量子力学算符，应在量子力学意义下予以研究。由于知识的欠缺，我们先半经典地研究角动量的相加。

角动量相加

$J$ , $L$ , $S$ 三个向量一起构成一个三角形, 根据三角形的性质(两边之和大于第三边, 两边只差小于第三边), 应满足:

$\left| l-s \right| \le j \le l + s$

这里 $l$ 是与轨道角动量 $L$ 对应的量子数, $s$ 是与自旋角动量 $S$ 对应的量子数, $j$ 是与总角动量 $J$ 对应的量子数。

总角动量 $J$ 也是角动量，和 $L$ , $S$ 一样它也满足:

$J^2 \left|j, m_j \right\rangle = j(j+1)\hbar^2 \left|j, m_j \right\rangle$

$J_z \left|j, m_j \right\rangle = m_j \hbar \left|j, m_j \right\rangle$

$j$ 的取值是整数，或半整数; $m_j = \pm j, \pm (j-1), ...$ ；共 $2j +1$ 种取值的可能性。

$j = l+s, l+s-1, ... , \left| l-s \right|$

（如果是两个一般的角动量 $L_1$ , $L_2$ 相加, 我们有总角动量量子数: $l = l_1 + l_2, l_1 + l_2 -1, ..., \left| l_1 - l_2 \right|$ ）

比如一个电子处在p轨道，它的总角动量就是:

$j = 1+1/2 = 3/2$ , 或 $j = 1-1/2 = 1/2$

总磁矩

$\mu = \mu_S + \mu_L = -g_L \frac{e}{2m} L - g_S \frac{e}{2m} S \neq \gamma J$

由于 $g_L = 1$ , $g_S =2$ , $\mu$ 与 $J$ 并不共线。

角动量相加和磁矩相加

我们现在的做法是先将 $\mu$ 投影到 $J$ 方向, 得到 $\mu_J$ , 然后再把 $\mu_J$ 写为 $- g_J\frac{e}{2m} J$ 的形式, 这样我们就得到了总角动量 $J$ 的朗德因子 $g_J$ 。

$\mu_J = \mu_S \cos (S, J) + \mu_L \cos (L, J)$

$\cos (S, J) = \frac{ J^2 + S^2 - L^2 }{ 2 \left|S\right| \cdot \left| J \right|}$

$\cos (L, J) = \frac{ J^2 + L^2 - S^2 }{ 2 \left|L \right| \cdot \left| J \right|}$

$\mu_J = \left( -g_S\frac{e}{2m}\left| S \right| \frac{ J^2 + S^2 - L^2 }{ 2 \left|S\right| \cdot \left| J \right|} - g_L \frac{e}{2m} \left| L \right| \frac{ J^2 + L^2 - S^2 }{ 2 \left|L \right| \cdot \left| J \right|} \right) \frac{J}{\left| J \right|}$

化简可得:

$\mu_J = \left( -g_S \frac{\mu_B}{\hbar} \frac{J^2 + S^2 - L^2}{2 J^2} - g_L \frac{\mu_B}{\hbar}\frac{J^2 + L^2 -S^2 }{2 J^2} \right) J = - g_J \frac{\mu_B}{\hbar} J$

朗德因子

得到：

$g_J = g_S \frac{J^2 + S^2 - L^2}{2 J^2} + g_L \frac{J^2 + L^2 - S^2}{2 J^2}$

考虑到 $g_S =2$ , $g_L = 1$ , 进一步可得,

$g_J = \frac{3}{2} + \frac{1}{2}\left( \frac{S^2 - L^2}{J^2} \right)$

在磁场中的能量

在原子物理中, 我们实际关心的是磁矩 $\mu_J$ 在已知磁场 $B$ 中的能量。

$U = - \mu_J \cdot B$

选磁场方向是 $z$ 轴,

$U = - \mu_J^z B = g_J \mu_B m_J B$

即,

$U = g_J m_J \mu_B B$

这里，

$m_J = J, J-1, ..., -J$

共 $2J +1$ 种取值的可能性。

人面猴
序言：七十年代末，一起剥皮案震惊了整个滨河市，随后出现的几起案子，更是在滨河造成了极大的恐慌，老刑警刘岩，带你破解...
沈念sama阅读 206,839评论 6赞 482
死咒
序言：滨河连续发生了三起死亡事件，死亡现场离奇诡异，居然都是意外死亡，警方通过查阅死者的电脑和手机，发现死者居然都...
沈念sama阅读 88,543评论 2赞 382
救了他两次的神仙让他今天三更去死
文/潘晓璐我一进店门，熙熙楼的掌柜王于贵愁眉苦脸地迎上来，“玉大人，你说我怎么就摊上这事。” “怎么了？”我有些...
开封第一讲书人阅读 153,116评论 0赞 344
道士缉凶录：失踪的卖姜人
文/不坏的土叔我叫张陵，是天一观的道长。经常有香客问我，道长，这世上最难降的妖魔是什么？我笑而不...
开封第一讲书人阅读 55,371评论 1赞 279
港岛之恋（遗憾婚礼）
正文为了忘掉前任，我火速办了婚礼，结果婚礼上，老公的妹妹穿的比我还像新娘。我一直安慰自己，他们只是感情好，可当我...
茶点故事阅读 64,384评论 5赞 374
恶毒庶女顶嫁案：这布局不是一般人想出来的
文/花漫我一把揭开白布。她就那样静静地躺着，像睡着了一般。火红的嫁衣衬着肌肤如雪。梳的纹丝不乱的头发上，一...
开封第一讲书人阅读 49,111评论 1赞 285
城市分裂传说
那天，我揣着相机与录音，去河边找鬼。笑死，一个胖子当着我的面吹牛，可吹牛的内容都是我干的。我是一名探鬼主播，决...
沈念sama阅读 38,416评论 3赞 400
双鸳鸯连环套：你想象不到人心有多黑
文/苍兰香墨我猛地睁开眼，长吁一口气：“原来是场噩梦啊……” “哼！你这毒妇竟也来了？” 一声冷哼从身侧响起，我...
开封第一讲书人阅读 37,053评论 0赞 259
万荣杀人案实录
序言：老挝万荣一对情侣失踪，失踪者是张志新（化名）和其女友刘颖，没想到半个月后，有当地人在树林里发现了一具尸体，经...
沈念sama阅读 43,558评论 1赞 300
护林员之死
正文独居荒郊野岭守林人离奇死亡，尸身上长有42处带血的脓包…… 初始之章·张勋以下内容为张勋视角年9月15日...
茶点故事阅读 36,007评论 2赞 325
白月光启示录
正文我和宋清朗相恋三年，在试婚纱的时候发现自己被绿了。大学时的朋友给我发了我未婚夫和他白月光在一起吃饭的照片。...
茶点故事阅读 38,117评论 1赞 334
活死人
序言：一个原本活蹦乱跳的男人离奇死亡，死状恐怖，灵堂内的尸体忽然破棺而出，到底是诈尸还是另有隐情，我是刑警宁泽，带...
沈念sama阅读 33,756评论 4赞 324
日本核电站爆炸内幕
正文年R本政府宣布，位于F岛的核电站，受9级特大地震影响，放射性物质发生泄漏。R本人自食恶果不足惜，却给世界环境...
茶点故事阅读 39,324评论 3赞 307
男人毒药：我在死后第九天来索命
文/蒙蒙一、第九天我趴在偏房一处隐蔽的房顶上张望。院中可真热闹，春花似锦、人声如沸。这庄子的主人今日做“春日...
开封第一讲书人阅读 30,315评论 0赞 19
一桩弑父案，背后竟有这般阴谋
文/苍兰香墨我抬头看了看天上的太阳。三九已至，却和暖如春，着一层夹袄步出监牢的瞬间，已是汗流浃背。一阵脚步声响...
开封第一讲书人阅读 31,539评论 1赞 262
情欲美人皮
我被黑心中介骗来泰国打工，没想到刚下飞机就差点儿被人妖公主榨干…… 1. 我叫王不留，地道东北人。一个月前我还...
沈念sama阅读 45,578评论 2赞 355
代替公主和亲
正文我出身青楼，却偏偏与公主长得像，于是被迫代替她去往敌国和亲。传闻我的和亲对象是个残疾皇子，可洞房花烛夜当晚...
茶点故事阅读 42,877评论 2赞 345