使用梯形法计算一二次函数的数值积分
$\int_{a}^{b}f(x)dx$
we can partition the integration interval $[a,b]$ into smaller subintervals,
and approximate the area under the curve for each subinterval by the area of
the trapezoid created by linearly interpolating between the two function values
at each end of the subinterval:

The blue line represents the function $f(x)$ and the red line
is the linear interpolation. By subdividing the interval $[a,b]$, the area under $f(x)$ can thus be approximated as the sum of the areas of all
the resulting trapezoids.
If we denote by $x_{i}$ ($i=0,\ldots,n,$ with $x_{0}=a$ and
$x_{n}=b$) the abscissas where the function is sampled, then
$$
\int_{a}{b}f(x)dx\approx\frac{1}{2}\sum_{i=1}{n}\left(x_{i}-x_{i-1}\right)\left(f(x_{i})+f(x_{i-1})\right).
$$
The common case of using equally spaced abscissas with spacing $h=(b-a)/n$ reads simply
$$
\int_{a}{b}f(x)dx\approx\frac{h}{2}\sum_{i=1}{n}\left(f(x_{i})+f(x_{i-1})\right).
$$
具体计算只需要这个公式
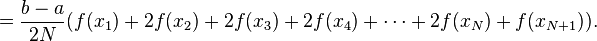
道理很简单,就是把积分区间分割为很多小块,用梯形替代,其实还是局部用直线近似代替曲线的思想。这里对此一元二次函数积分,并与python模块积分制对比(精确值为4.5)用以验证。
$$
\int_a^b (x^2 - 3x + 2) dx
$$
from scipy import integrate
def f(x):
return x*x - 3*x + 2
def trape(f,a,b,n=100):
f = np.vectorize(f) # can apply on vector
h = float(b - a)/n
arr = f(np.linspace(a,b,n+1))
return (h/2.)*(2*arr.sum() - arr[0] - arr[-1])
def quad(f,a,b):
return integrate.quad(f,a,b)[0] # compare with python library result
a, b = -1, 2
print trape(f,a,b)
print quad(f,a,b)
4.50045
4.5