练习:Sqrt函数可视化实现
本次练习主要是熟练numpy和matplotlib的使用,通过手写Sqrt的实现,通过可视化对比手写函数与系统自带函数之间区别。
主要实现思路是:牛顿法
下面简单介绍一下牛顿法:(参考博客,参考知乎) 首先,有函数f(x) = x²,假设num是f(x)的近似值,那么num最接近f(x),就有f(x)-num=0,也就是x² - num = 0.
那么如果画图,就是要求g(x)=x² - num 与g(x)=0 的最近点。
极限公式:
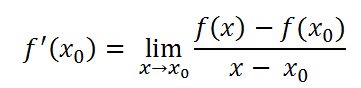
因此有:
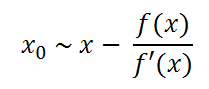
从几何图形上看,因为导数是切线,通过不断迭代,导数与x轴的交点会不断逼近x0。
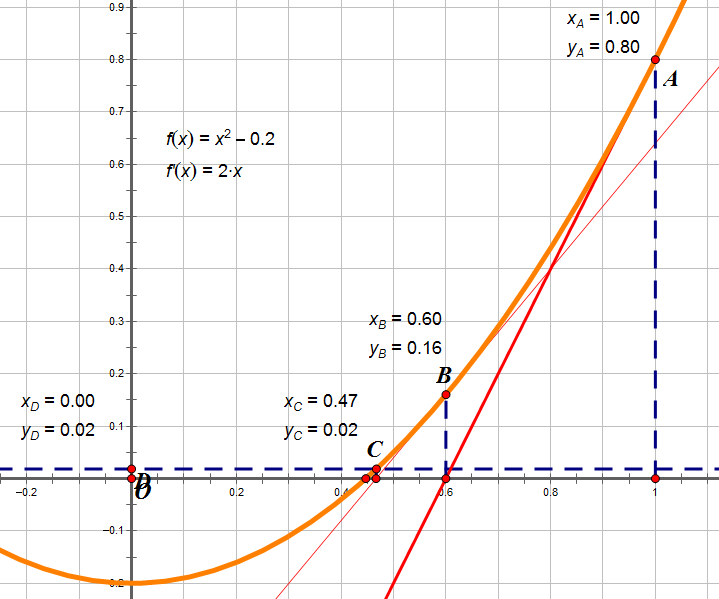
从上图我们可以看出,第一次A点,画出A的切线,在X轴上有交点,这个交点投影到曲线上,找到点B,同理,B点又做切线,找到一个交点,交点又投影到曲线得到点C,逐渐接近X0。
由前面的极限公式得出:
$$f'(x_n) = \frac{dy}{dx} = \frac{f(x_n)}{x_n - x_{n+1}}$$
推导得出:
$$x_{n+1} = x_n -\frac{f(x_n)}{f'(x_n)}$$
ok,到这里我们举一个实例
假设m=2,那么就有:
最终得出以下图例:手写的sqrt函数与系统自带的基本没有区别

、
# -*- coding:utf-8 -*-
# /usr/bin/python
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import math
def func(a):
if a < 1e-6: #小于0.000001,直接返回0
return 0
last = a
c = a / 2 #该值一定程度上影响迭代次数
while math.fabs(c - last) > 1e-6:#精度控制
last = c
c = (c + a/c) / 2
return c
if __name__ == '__main__':
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False #保证win系统图片上的中文显示正常
x = np.linspace(0, 30, num=50) #0-30均分50份
func_ = np.frompyfunc(func, 1, 1) #转换为ufunc函数方便使用
y_h = func_(x)
y_s = np.sqrt(x)#调用系统自带函数求值
plt.figure(figsize=(10, 6), facecolor='w')#设置图大小和背景色
plt.plot(x,y_h, 'ro-',label='手写', lw=2, markersize=6)#(画出x与y_h的曲线,用红色小圆圈标记(x,y)在图上的位置,
#label下面legend函数要调用的,相当于注明这条曲线的意义,lw线宽2,小圆点6)
plt.plot(x,y_s, 'b-',label='系统自带', lw=2, markersize=6)
plt.grid(b=True, ls=':')#显示网格
plt.legend(loc='lower right')#选取两条曲线的注明所在方位
plt.xlabel('X', fontsize=16)#坐标轴上的内容及大小
plt.ylabel('Y', fontsize=16)
plt.title('牛顿法计算平方根', fontsize=18)
plt.show()
关于分母的取值影响迭代次数的研究
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import math
def func(b):
if b < 1e-6:
return 0
a = 1000
last = a
c = a / b
count = 0
while math.fabs(c - last) > 1e-6:
last = c
c = (c + a/c) / 2
count = count + 1
return count
if __name__ == '__main__':
x = np.linspace(2, 500, num=100)
func_ = np.frompyfunc(func, 1, 1)
y = func_(x)
print(x,y)
>>>[9 7 6 5 5 4 3 4 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 7 7 7 7 7 7 7 7 7 7 7 7 7 7
7 7 7 7 7 7 7 7 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8
8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 9 9 9 9 9 9 9 9 9 9]