# 前言
在canvas中实现图片移动、实现矩形移动,大家可能看的很多了。但是我为什么还要去写这样的一篇文章呢,因为笔者曾经做到3维图形下的移动。包括移动一个立方体上的一条边线、一个面、移动多边形的一个点。最近一直在写canvas的相关的文章,想着复习下,读完本篇文章你可以学到,通过移动矩形的一个点, 一个条边线,以及整个面的移动。本篇文章从浅到深,希望你耐心读下去。
# 面的移动
试想一下,在canvas 下实现移动功能。第一步肯定创建canvas 并对canvas 添加move 事件, 这样我们实时获取到我们鼠标的位置,然后我们只需要不断的清除画布,然后重新画矩形。就OK了,面的移动初步实现。我在下面写点的移动会把这里重写了, 这里先写个快速简易版本的。
```js
const canvas = document.getElementById('canvas');
const ctx = canvas.getContext('2d');
const width = 100;
const height = 100;
drawRect();
function drawRect(x = 10,y = 10, scale = 1) {
ctx.clearRect( 0, 0, 1800, 800 );
const halfwidth = width * scale / 2;
const halfheight = height * scale / 2;
ctx.strokeRect(x - halfwidth, y - halfheight,width * scale, height * scale)
}
let isMove = true;
canvas.addEventListener('mousemove',(e)=>{
if(!isMove) {
return
}
const x = e.clientX;
const y = e.clientY;
drawRect(x,y)
})
canvas.addEventListener('click',(e)=> {
isMove = !isMove;
});
```
isMove变量就是个开关,我们总不能一直移动吧,那也太累了,鼠标点击的就暂停。 对于上文为什么要x - halfwidth, y - halfheight
这里和大家解释下: strokeRect 是从矩形的左上角开始画的,但是呢我想把矩形放在鼠标中心位置, 所以做一个宽度和高度相减就可以完美展示了。
# 点的移动
首先第一个问题就是? 我们怎么知道我们选择的是哪一个点呢,这里我做了一个简单的判断就是通过判断鼠标点击的位置和矩形的每个点的位置作比较,看看哪一个离得近就作为目标点。因为我们2d其实点的移动其实也就是找这个点关联的线段, 所以我们只需要重新生成关联的线段就好了,但是这里有一个比较难以处理的地方? 就是移动一个半圆? 如果我们移动半圆的断点, 这里就涉及到圆弧的改变了,可能变成椭圆弧或者说用二阶、三阶贝塞尔曲线去表达。还有就是移动一个图形和画布上其他图形形成了切割? 是不是也要切割算法?其实可以用**Clipper**去求交并差,感兴趣的同学可以自行去了解一下,但是这些不在本篇文章所想要阐述中。 本篇文章所有的例子(只支持直线也就是LineSegment)。
OK,我们第一步我们得去重新表达矩形,因为他不够通用准确的是重新表达四边形, 矩形和正方形只是其中的特列。这里我给出原因? 为什么呢一个很简答的case,移动四边形的一个点,他可能变成下面这样:
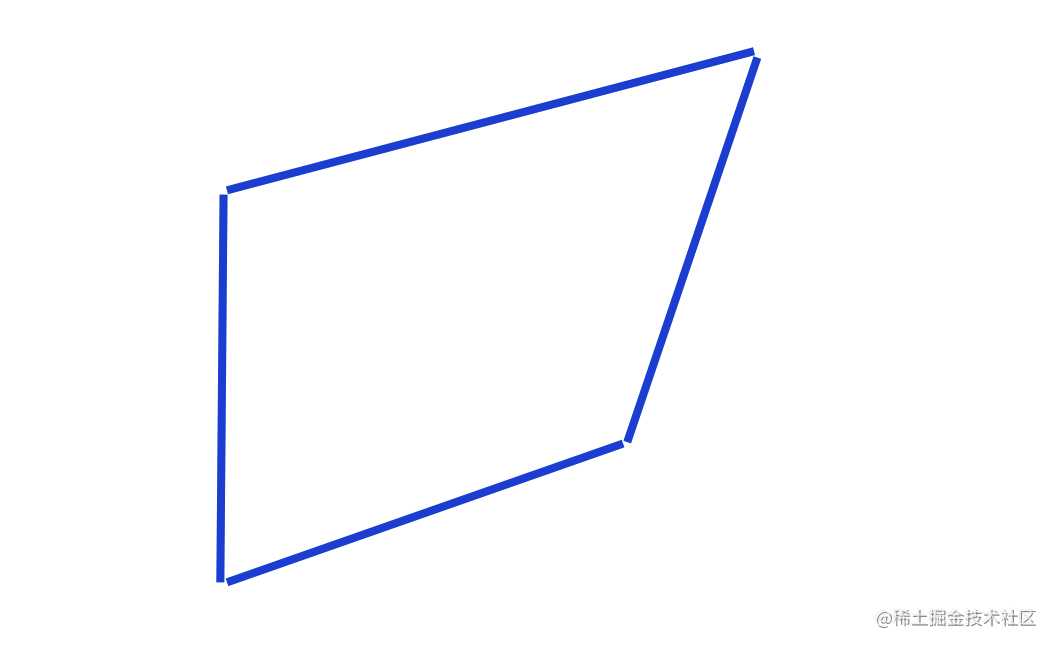
ok 为了下面好表达我们新建一个Point2d这个类, 将画布上的每一个点都用一个实例去表示。
```js
class Point2d {
constructor(x,y) {
this.x = x || 0;
this.y = y || 0;
}
clone() {
return this.constructor(this.x, this.y);
}
add(v) {
this.x += v.x;
this.y += v.y
return this;
}
random() {
this.x = Math.random() *1800;
this.y = Math.random() * 800;
return this
}
}
```
接下来我们就随便在画布上一鼠标的位置分别加上矩形的长度和宽度,画出矩形。 代码如下:
```js
function drawFourPolygon(x, y ,width = 50, height = 50) {
ctx.clearRect( 0, 0, 1800, 800 );
ctx.beginPath();
ctx.moveTo(x- width /2, y - height/2)
ctx.lineTo(x+ width / 2, y -height/2 )
ctx.lineTo(x+ width / 2, y + height/2 )
ctx.lineTo(x - width / 2, y + height/2 )
ctx.closePath()
ctx.stroke()
}
```
为了交互更加完美, 鼠标第一次点击确定移动的开始点, 然后 鼠标不停地移动就是移动的终止点, 这样就确定了一个向量。 这里为了移动的时候更加明显我增加了虚线功能,代码如下
```js
function drawDashLine(start, end) {
if (!start || !end) {
return
}
ctx.strokeStyle = 'red';
ctx.setLineDash( [5, 10] );
ctx.beginPath();
ctx.moveTo( start.x, start.y );
ctx.lineTo( end.x, end.y );
ctx.closePath()
ctx.stroke();
}
```
这里用到的就是canvas setLineDash 这个api 参数的含义,实线的距离5、空白的距离10 如此往复的走下去形成虚线。start和end 就是鼠标点击确定的就是start 点, 然后鼠标不停的移动就是end点。 这里有一个小提醒就是我鼠标移动的过程中先画了虚线,然后又画了矩形所以呢? 矩形我们还是实线。我们这里对画矩形代码做了修改,还是把虚线还原过来。
代码如下:
```js
ctx.setLineDash([]);
```
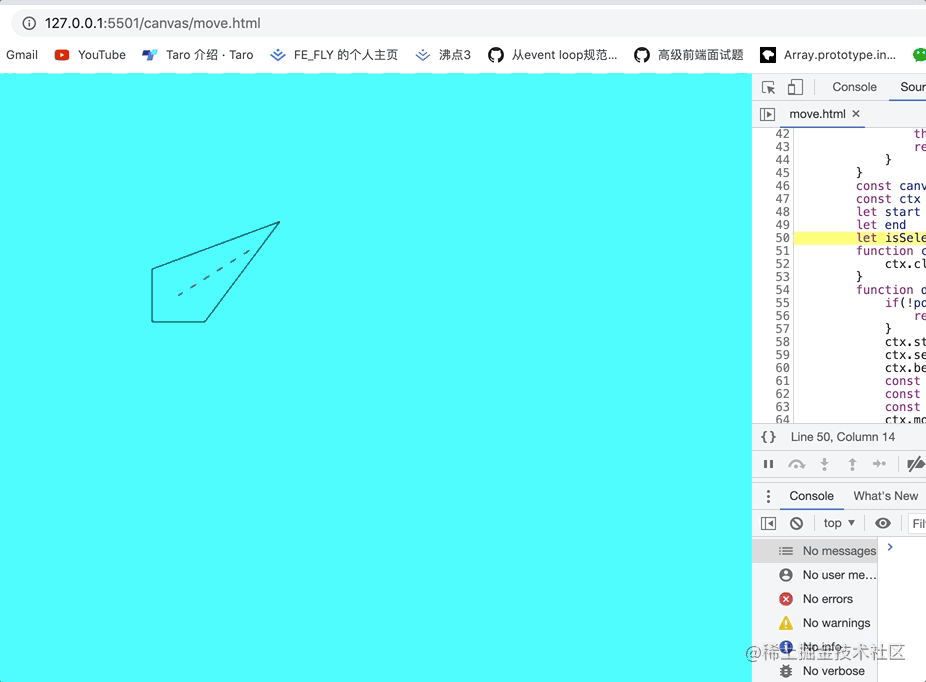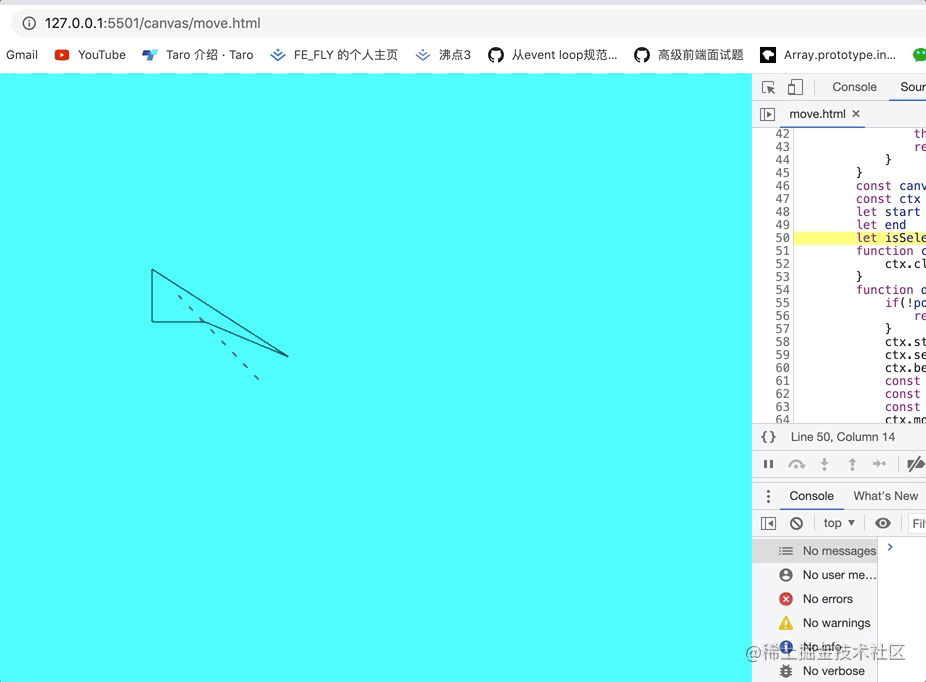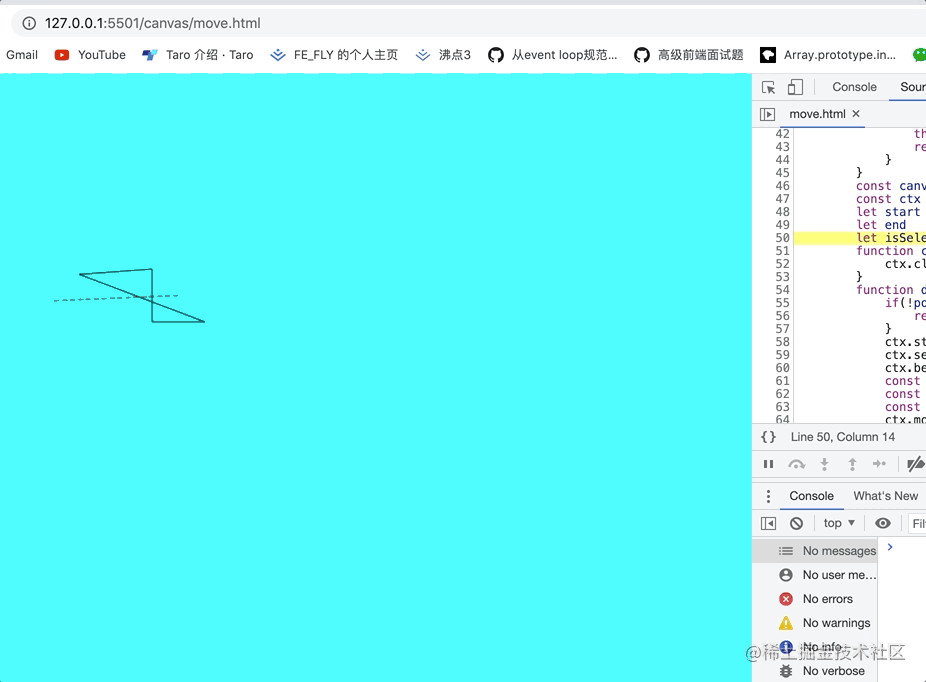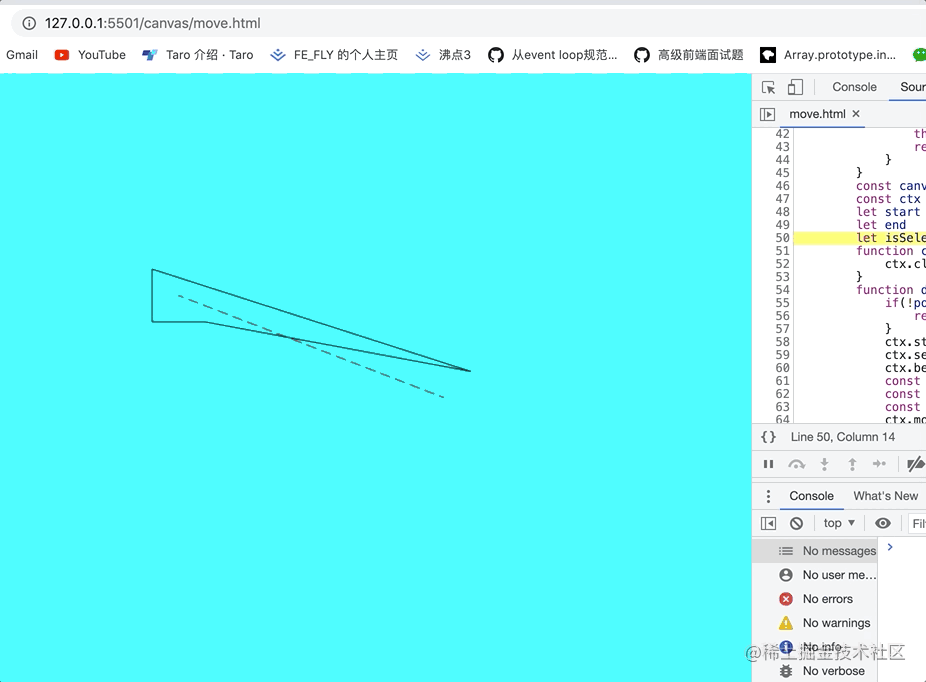
OK整体的交互出来了,我先给大家看下效果:

是不是有点感觉了哈哈哈?从画面上看这还是整体的移动不是点的移动, 由于我画的图形以鼠标点击的那个点去画矩形的,我的下一篇文章会给大家介绍不规则多边形点的移动,本篇文章我们还是假设我移动的是**右上角的那个点**。OK**我们由移动的开始点和结束点, 可以得到一个移动的向量, 所以我们只要将要移动的点 和这个向量相加。这样我们是不是实现了点的移动。**
```js
const moveVec = end.clone().sub(start);
const rightTop = new Point2d(x+ width / 2, y - height/2).clone().add(moveVec)
```
这里我改变了右上角的点,但是呢有一个问题就是我们点击也是走的同一个函数,所以我们得加个开关去判断下,主要是用来判读是第一次点击还是移动就好了代码如下:
```js
ctx.lineTo(isSelect ? rightTop.x : x+ width / 2, isSelect ? rightTop.y : y height/2)
// 看下click和move 事件 开关就是isSelect这个变量
canvas.addEventListener('mousemove',(e)=>{
if(!isMove) {
return
}
const x = e.clientX;
const y = e.clientY;
clearRect();
end = new Point2d(x,y);
drawDashLine(start,end);
drawFourPolygon(start)
})
canvas.addEventListener('click',(e)=> {
// 这是一个每次清除画布的函数
clearRect()
isMove = !isMove;
const x = e.clientX;
const y = e.clientY;
start = new Point2d(x,y);
drawFourPolygon(start)
isSelect = true;
});
```
效果图如下:
哈哈哈是不是十分的丝滑和流畅, 发现canvas 的画图的性能还是非常不错的。但是还是有一个问题就是,确定结果,看上面代码我们确定结果是有问题的。 所以我以按住alt键结束为确定结果这就十分完美了,代码就不在这里展现了。
# 线的移动
有了点的移动,线的移动就显示的十分简单。 线的移动其实就是对应的点的移动。 我们以右边这条线为例子: 代码改写如下:
```js
function drawFourPolygon( point, width = 50, height = 50) {
if(!point) {
return
}
ctx.strokeStyle = 'black'
ctx.setLineDash([]);
ctx.beginPath();
const { x, y } = point;
const moveVec = end.clone().sub(start);
// 其实就是 右上和右下这两个点同时移动
const rightTop = new Point2d(x+ width / 2, y - height/2).clone().add(moveVec)
const rightBottom = new Point2d(x+ width / 2, y + height/2).clone().add(moveVec)
ctx.moveTo(x- width /2, y - height/2)
ctx.lineTo(isSelect ? rightTop.x : x+ width / 2, isSelect ? rightTop.y : y - height/2)
ctx.lineTo(isSelect ? rightBottom.x : x+ width / 2, isSelect ? rightBottom.y : y + height/2)
ctx.lineTo(x - width / 2, y + height/2 )
ctx.closePath()
ctx.stroke()
}
```
我们看下效果图:

# 总结
本篇文章主要介绍的2d图形下最基本的变化**移动**,无论是线的移动还是面的移动最终都是点的移动。其实移动除了用向量表示还可以用矩阵, 或者说我们旋转移动缩放等等命令都可以用矩阵变化表示。 最后还是感谢大家看到最后,码字不容易,如果看了对你有帮助的, 欢迎点个赞👍和关注。 你的支持是我持续更新好文章的最大动力。 所有代码都在我的[github](https://github.com/wzf1997/blog)上。欢迎大家star。
公众号: 前端图形 持续分享前端可视化知识