前面一篇文章贝叶斯统计:初学指南介绍了最简单的 Metropolis 采样方法,本文将介绍另一种采样 Metropolis-Hastings ,并且会对前文介绍的例子给出证明,为什么 Metropolis 采样work。
回顾
我们简单的回顾下前文的内容,我们首先介绍了为什么需要有mcmc,假设有一个贝叶斯公式:
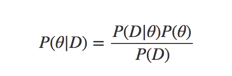
我们为了求得后验分布,需要去计算P(D)
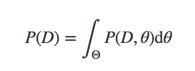
但是由于好多分布其参数空间非常大,很难计算P(D),于是就提出了数值逼近的方法,但是由于参数空间巨大,我们就要高效的去采样,于是就有了mcmc方法,mcmc方法的一般套路:
- 先在参数空间中选择一个
- 在参数空间中提议一个新的位置
- 根据先验信息和观测数据决定接收或者拒绝
- 如果接收跳跃,则跳转到新的位置,并且返回到 step1
- 如果拒绝,则保持当前位置并返回到 step1
- 连续采用一系列点,最后返回接受的点集合
不同的 mcmc 算法的区别在于怎么选择跳跃方式已经如何决定是否跳跃,前面一篇贝叶斯统计:初学指南介绍了 Metropolis 对上述过程的处理,本文会介绍 Metropolis-Hastings 方法。
Metropolis-Hastings
先介绍算法的整个流程:

下面开始进行回答,为什么上面这个过程work?
首先我们需要上面的过程中,我们采样出来是x是服从概率分布π(x)的,然后我们采样的函数是一个k(x|x),那就有下面的公式:
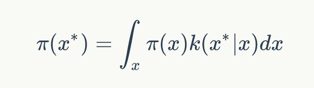
$$
\pi(x^) =
\int_{x}\pi(x)k(x^*|x)dx
$$
上面公式保证了如果我们按照k进行采样,能够保证新的采样点和原先的点都是服从同一个分布的。
下面我们来证明如果细致平稳条件成立:
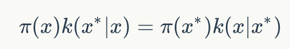
$$
\pi(x)k(x^|x) = \pi(x^)k(x|x^)
$$
则上面的积分也成立。
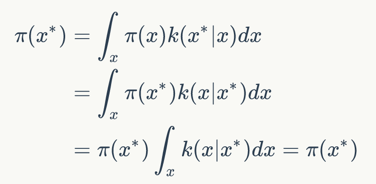
$$
\begin{align}
\pi(x^) & = \int_{x}\pi(x)k(x^|x)dx \
& = \int_{x} \pi(x^)k(x|x^)dx \
& = \pi(x^) \int_{x} k(x|x^)dx = \pi(x^)
\end{align}
$$
现在我们就证明了细致平稳条件能保证x都服从同一分布。
下面我们继续来看如何选择k分布。
在 Metropolis-Hastings 中我们采取下面的策略:
- 从q(x|x)中采样x
-
计算接收率
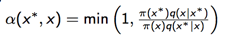
下面我们来证明上面的选取的k满足细致平稳条件:

下面我们来看下q(.)函数的选择,q(.)函数的选择一般有两种:
- 对称,如高斯分布,均匀分布,这种情况下称为随机游走
- 非对称:如log-normal,倾向于选择大的x值
下面是接收函数,我们可以得到下面两个点:
-
采样值倾向于选择高概率的点,因为

-
我们不希望采样点来回震荡,因为:
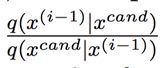
在上面一篇文章介绍的 Metropolis 算法中,q(.)函数就是对称的,此时接收率就是:
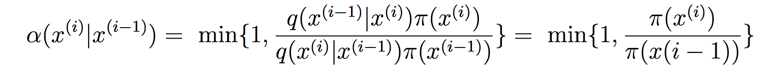
此时完全就是变为衡量哪个参数更能描述数据了,更细致的说明可以看前面一篇文章贝叶斯统计:初学指南。
例子
假设我们有两个时序数据,xi,yi,其相关性为ρ,现在两个之间的服从一个二元高斯分布:
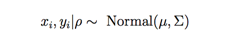

为简单起见,我们假设σxx , σyy = 1。
此时我们可以写出似然概率:
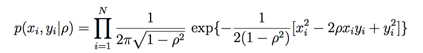
然后先验概率如下:

最后我们可以得到后验概率的近似:

下面我们就要通过mh方法来做的。
我们选择q(.)为均匀分布:
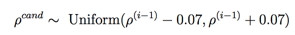
此时计算接受率则只计算p(ρ)即可,可以看代码:
rho_candidate=uniform.rvs(rho-0.07,2*0.07)
accept=-3./2*log(1.-rho_candidate**2) - N*log((1.-rho_candidate**2)**(1./2)) - sum(1./(2.*(1.-rho_candidate**2))*(x**2-2.*rho_candidate*x*y+y**2))
计算的是log,方便计算,完整的代码见mh
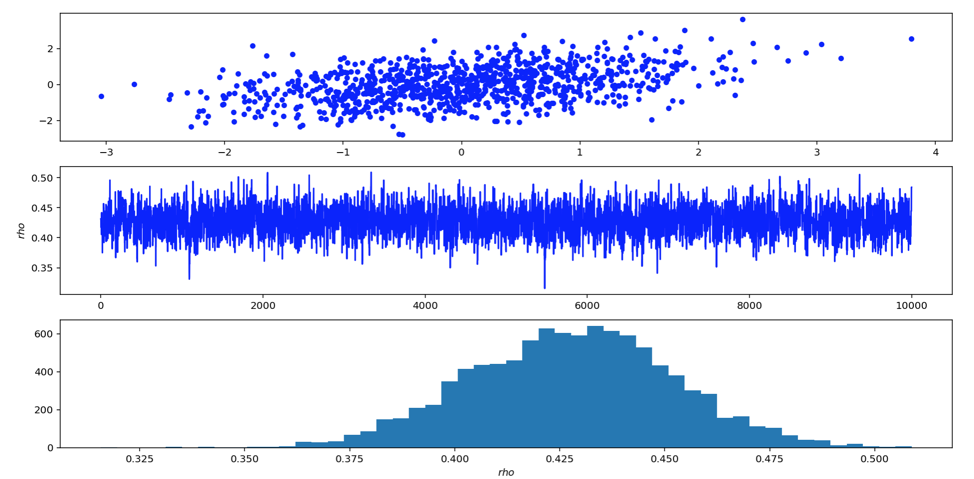
可以看到我们采样后的ρ均值差不多就是0.4,符合我们的实际数据。
总结
文本介绍了MH算法,并且给出了为什么MH算法的证明,最后以一个简单例子结尾,下面一篇我会继续介绍Gibbs Sampling的,欢迎关注。
参考
Bayesian Inference: Metropolis-Hastings Sampling
你的鼓励是我继续写下去的动力,期待我们共同进步。
