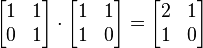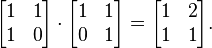抽象代数作为数学的一门学科,主要研究对象是代数结构,比如群、环、域、模、向量空间和代数。事实上,对抽象代数的研究是应数学更严格化的要求而发展起来的。对抽象代数的研究还使人们形成了对全部数学和自然科学的基础性逻辑假设(的复杂性)的整体认识,现今,几乎没有那一个数学分支用不到代数学的结论。此外,随着抽象代数的发展,代数学家们发现:明显不同的逻辑结构通过类比可以得到一个很简练的由公理构成的核心。这对深入研究代数的数学家是有益的,并赋予他们更大的本领。
20世纪初,抽象代数有时也称为现代代数,近世代数。
参见:http://zh.wikipedia.org/wiki/%E6%8A%BD%E8%B1%A1%E4%BB%A3%E6%95%B0
1. 代数结构:
集U上定义二元运算形成的系统称为代数系统,如果对于任意a,b∈U,恒有(a·b)∈U。
二元运算属于数学运算的一种。二元运算需要三个元素:二元运算符以及该运算符作用的两个变量。
给定集合A,二元函数F: A×A→A称为集合A上的二元运算。
可以看出,“集合A上的二元运算”这样的提法暗示了该运算在A上封闭。
二元运算可推广至多元运算F,则相应的封闭性要求则改为:对于任意a,b,c,d,……∈U,恒有F(a,b,c,d,……)∈U。
有的书上对封闭性未作要求,并称之为广群。运算f是一个从A×B→C的映射,若A=B=C,则称运算f是封闭的。
以下是集中代数结构:
2. 群
在数学中,群是一种代数结构,由一个集合以及一个二元运算所组成。
一个群必须满足一些被称为“群公理”的条件
也就是:(1)封闭性(代数结构就具备)、(2)结合律、(3)单位元和(4)逆元。
例如,整数配备上加法运算就形成一个群。(Z, +)是一个群。
群在数学内外各个领域中是无处不在的,这使得它们成为当代数学的组成的中心原理。
群的例子:
2.1 第一个例子:(Z, +):
最常见的群之一是整数集Z,它由以下数组成:
..., −4, −3, −2, −1, 0, 1, 2, 3, 4, ...
下列整数加法的性质,可以作为抽象的群公理的模型。
(1)封闭性:对于任何两个整数a和b,它们的和a+b也是整数。换句话说,在任何时候,把两个整数相加都能得出整数的结果。这个性质叫做在加法下封闭。
(2)结合律:对于任何整数a,b和c,(a+b) +c=a+(b+c)。用话语来表达,先把a加到b,然后把它们的和加到c,所得到的结果与把a加到b与c的和是相等的。这个性质叫做结合律。
(3)单位元(既是左单位元又是右单位元):如果a是任何整数,那么0 +a=a+ 0 =a。零叫做加法的单位元,因为把它加到任何整数都得到相同的整数。
(4)逆元:对于任何整数a,存在另一个整数b使得a+b=b+a= 0。整数b叫做整数a的逆元,记为−a。
2.2 一般定义:
群是一个集合G,连同一个运算"·",它结合任何两个元素a和b而形成另一个元素,记为a·b。符号"·"是对具体给出的运算,比如上面加法的一般的占位符。要具备成为群的资格,这个集合和运算(G,·)必须满足叫做群公理的四个要求:
(1).封闭性。对于所有G中a,b,运算a·b的结果也在G中。
(2).结合性。对于所有G中的a,b和c,等式 (a·b)·c=a· (b·c)成立。
(3).单位元。存在G中的一个元素e,使得对于所有G中的元素a,等式e·a=a·e=a成立。
(4).逆元。对于每个G中的a,存在G中的一个元素b使得a·b=b·a=e,这里的e是单位元。
进行群运算的次序是重要的。换句话说,把元素a与元素b结合,所得到的结果不一定与把元素b与元素a结合相同;等式
a·b=b·a
不一定恒成立。这个等式在整数于加法下的群中总是成立,因为对于任何两个整数都有a+b=b+a(加法的交换律)。但是在一般的群中不总是成立。使等式a·b=b·a总是成立的群叫做阿贝尔群(以挪威数学家尼尔斯·阿贝尔命名)。因此,整数加法群是阿贝尔群,但一般群群不一定是。
2.3 阿贝尔群
阿贝尔群也称为交换群或可交换群,它是满足其元素的运算不依赖于它们的次序(交换律公理)的群。阿贝尔群推广了整数集合的加法运算。阿贝尔群以挪威数学家尼尔斯·阿贝尔命名。
阿贝尔群是有着群运算符合交换律性质的群,因此阿贝尔群也被称为交换群。它由自身的集合G和二元运算* 构成。它除了满足一般的群公理,即运算的结合律、G有单位元、所有G的元素都有逆元之外,还满足交换律公理:
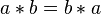
而群运算不满足交换律的群被称为“非阿贝尔群”,或“非交换群”。
2.4 环
环(Ring)的定义类似于可交换群,只不过在原来“+”的基础上又增添另一种运算“·”(注意我们这里所说的 + 与 · 一般不是我们所熟知的四则运算加法和乘法)。在抽象代数中,研究环的分支为环论。
集合R和定义于其上的二元运算 + 和·,(R, +, ·)构成一个环,若它们满足:
(1) (R, +)形成一个交换群,也就是一个阿贝尔群。其单位元称为零元,记作‘0’。即:
①(R, +)是封闭的
②(a + b) = (b + a)
③(a + b) + c = a + (b + c)
④0 + a = a + 0 = a
⑤∀a ∃(−a) 满足 a + −a = −a + a = 0
(2) (R, ·)形成一个半群,即:
①(a·b)·c = a·(b·c)
②(R, ·)是封闭的
(3)乘法关于加法满足分配律:
①a·(b + c) = (a·b) + (a·c)
②(a + b)·c = (a·c) + (b·c)
其中,乘法运算符·常被省略,所以 a·b 可简写为 ab。 此外,乘法是比加法优先的运算,所以 a + bc 其实是 a + (b·c)。
补:交换环(commutative ring)是乘法运算满足交换律的环
环是一个集合R带有两个二元运算,即将环中的任意两个元素变为第三个的运算。他们称为加法与乘法,通常记作 + 与 ⋅ ,例如a+b与a⋅b。为了形成一个群这两个运算需满足一些性质:环在加法下是一个阿贝尔群,在乘法下为一个幺半群,使得乘法对加法有分配律,即a⋅ (b+c) = (a⋅b) + (a⋅c)。关于加法与乘法的单位元素分别记作 0 和 1。
另外如果乘法也是交换的,即
a⋅b=b⋅a,
环R称为交换的。
一个重要的例子,在某种意义下是最关键的,是带有加法与乘法两个运算的整数环Z。因为整数乘法是一个交换运算,这是一个交换环。通常记作Z,是德语词Zahlen(数)的缩写。
2.5 域
域是一种交换环(F, +, *),当中加法单位元(0)不等于乘法单位元(1),且所有非零元素有乘法逆元。
一个域是每个非零元素a是可逆的交换环,即有一个乘法逆b使得a⋅b= 1。从而,由定义知任何域是一个交换环。有理数、实数、复数都是域。