在一个没有任何电荷的无限大空间中,电势的分布遵循Laplace's equation:
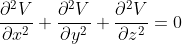
接下来的讨论中,我们将针对拉普拉斯方程展开讨论,并将其用python代码模拟出来。
公式推导
在点(i,j,k)上我们对x的偏分可以写作:
-v(i,j,k)}{\Delta x})
或者:
-V(i-1,j,k)}{\Delta x})
因此,容易得到:
-V(i,j,k)}{\Delta x}-\frac{V(i,j,k)-V(i-1,j,k)}{\Delta x}])
再稍微做一点运算,得到:
+V(i-1,j,k)-2V(i,j,k)}{(\Delta x)^2})
对y,z方向上的偏分运算也是类似的,在此就不做推导,再将上面的式子代入Laplace's equation中,得到:
=\frac{1}{6}[V(i+1,j,k)+V(i-1,j,k)+V(i,j+1,k)+V(i,j-1,k)+V(i,j,k+1)+V(i.j,k-1)])
我们先考虑平面的情况,因此上式改为:
=\frac{1}{4}[V(i+1,j,k)+V(i-1,j,k)+V(i,j+1,k)+V(i,j-1,k)])
具体算法
我们首先预设一些初始值,并用上式不断的迭代这些值,直到这些值满足Laplace's equation
- set initial value of laplace's V to be zero.
- loop through all points(i,j) except the boundary,where values of V_n are fixed by the boundary conditions.
- \ and\ \triangle V\ to\the\ calling\ program)
code
# -*- coding: utf-8 -*-
# author:Ricardo Zi Tseng #
# electric potentials and fields:Laplace's Equation #
import math
import numpy as np
import matplotlib.pyplot as pl
class Laplace(object):
def __init__(self):
self.V = np.array([[-1.00,-0.67,-0.33,0.00,0.33,0.67,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.67,-0.33,0.00,0.33,0.67,1.00]])
self.temp_V = np.array([[-1.00,-0.67,-0.33,0.00,0.33,0.67,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.67,-0.33,0.00,0.33,0.67,1.00]])
def Run(self):
loop = True
# sum_value = 0
k = 0
while(loop):
temp = self.V
for i in range(1,6):
for j in range(1,6):
self.temp_V[i,j] = (self.V[i-1,j] + self.V[i+1,j] + self.V[i,j-1] + self.V[i,j+1])/4
# sum_value = sum_value + abs(self.temp_V[i,j]-self.V[i,j])
self.V = self.temp_V
# sum_value = sum_value/49
k = k + 1
if k > 1:
# if sum_value < 0.0001:
loop = False
def Show(self):
print(self.V)
tips:
由于python中的list需要考虑到浅copy和深copy的问题,为了减少不必要的麻烦与错误,我直接将程序中的所有list转化为numpy中的矩阵了,效果理想。
运算结果
我们首先设定初始值:
[-1.00,-0.67,-0.33,0.00,0.33,0.67,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.00,-0.00,0.00,0.00,0.00,1.00],
[-1.00,-0.67,-0.33,0.00,0.33,0.67,1.00]
- 第一次迭代
[[-1. -0.67 -0.33 0. 0.33 0.67 1. ]
[-1. -0.500625 -0.20765625 -0.03128906 0.17905273 0.52476318 1. ]
[-1. -0.43765625 -0.16132812 -0.0481543 0.09522461 0.46749695 1. ]
[-1. -0.42191406 -0.14581055 -0.04849121 0.07418335 0.44792007 1. ]
[-1. -0.45985352 -0.17204102 -0.05513306 0.08788757 0.48832691 1. ]
[-1. -0.55308838 -0.26378235 -0.05910385 0.19407093 0.58809946 1. ]
[-1. -0.67 -0.33 0. 0.33 0.67 1. ]]
- 第十次迭代
[[-1. -0.67 -0.33 0. 0.33 0.67 1. ]
[-1. -0.6715042 -0.33950297 -0.00741688 0.32681153 0.66439877 1. ]
[-1. -0.67337165 -0.34377344 -0.01122901 0.32445917 0.66239877 1. ]
[-1. -0.67355945 -0.34410226 -0.0113158 0.32455897 0.66232886 1. ]
[-1. -0.6720973 -0.34143181 -0.00852736 0.32665836 0.66353442 1. ]
[-1. -0.67005562 -0.33680115 -0.0042711 0.32938443 0.66572971 1. ]
[-1. -0.67 -0.33 0. 0.33 0.67 1. ]]
- 第十五次迭代
[[-1. -0.67 -0.33 0. 0.33 0.67 1. ]
[-1. -0.66853725 -0.3344115 -0.0017874 0.33129 0.66668929 1. ]
[-1. -0.66858639 -0.33585108 -0.00268339 0.33116261 0.6658073 1. ]
[-1. -0.66850175 -0.33594729 -0.00268531 0.33125373 0.66571686 1. ]
[-1. -0.66815249 -0.33519058 -0.00201488 0.33166784 0.6660607 1. ]
[-1. -0.66803195 -0.33364162 -0.0010076 0.33187959 0.66698507 1. ]
[-1. -0.67 -0.33 0. 0.33 0.67 1. ]]
差不多到第十五次迭代的时候,就能算到理想值了。
一些较为复杂的情况
假设在无限大空间中有一块电势为1的平板,试试计算一下它周围的电势分布与场分布
等势线

三维图


电场分布

假设在无限大平面上有两块电势分别为1和-1的平板,试作出这个体系的电势图和电场分布



总结
总的来说,这道题目的算法并不复杂,难的地方可能在python值传递、浅copy和深copy的问题上,与其花大量时间研究python的内部机制,倒不如直接用numpy中的矩阵进行计算,也能大大简化代码。
致谢
绘图部分的代码参考了华杨学姐的代码