上一篇的迷宫问题难倒了很多人,对于初学者这个相对综合的问题可能的确有点难,不过并非完成不了。我们今天就来看看初学者如何用最基础的方法解决这个问题。
1. 题目

如图所示,有一个6 * 6的迷宫,左上角为入口,右下角为出口。图中0的位置可以走,1的位置不能走。请编程找出唯一的一条通过迷宫的路。
2. 分析
2.1 经典解法
这道题是一个C语言编程中的经典题目,网上的答案有很多。有人还真去查了,但结果有点崩溃,他们看到的是:回溯、递归、堆栈、迭代、DFS这些初学者根本没怎么听过的关键词。那些没有注释的例程也是怎么也看不懂。其实,就因为题目太过经典,所以才有各种五花八门的解法。
总结一下,主流的解法就两种:
- DFS 深度优先遍历法
通过递归的方式不断从入口寻找下一个可行的点,依次执行下去。一旦发现死路就退回到上一个点重新寻找新路线。
理论上遍历了所有可能的路线之后,正确的路线一定能够找到。
- BFS 广度优先遍历法
这个算法的特点是不需要递归,需要自己维护一个顺序表,之后通过循环同时寻找和当前点相连的每一个联通的点,直到找到出口。
这个算法的特点是不需要回退。
以上两种是数据结构中的经典算法,不过我们今天要讲的并非这两种。所以千万不要被吓到了。
2.2 功能分解
首先说一下,经典的编程问题,每个都有经典的解法。这些解法是很多人共同总结出来的可以解决一类问题的最优算法。然而,对于某一个具体的问题,这些算法并不一定是最优的或者说最简单的。
这道题就是这样。迷宫问题最大的难点就是它有很多岔路是走不通的。那我们想想,如果迷宫没有岔路你会做吗?

相信大部分人都能解决。那么这就是我们的目标。
- 功能一:迷宫打印
把迷宫打印在屏幕上,其实是二维数组的打印。
- 功能二:迷宫剪支
把迷宫中所有的死路删除。
- 功能三:标记正确路线
最后我们需要把正确的路线打印在屏幕中。
从步骤上说,我们要做的就是这三件事。要把大象放冰箱,总共分几步,分三步。
3. 代码框架
依然是堆积木,我们今天先写main函数的框架,之后把积木填进去。
void main()
{
int i, j, k;
int maze[MAX_SIZE][MAX_SIZE] =
{
{ 0, 1, 0, 1, 1, 1 },
{ 0, 0, 0, 1, 0, 1 },
{ 0, 1, 1, 0, 0, 0 },
{ 0, 1, 1, 0, 1, 0 },
{ 0, 0, 0, 0, 1, 0 },
{ 0, 1, 1, 1, 1, 0 }
};
// 打印原始迷宫
printf("原始迷宫:\n");
// 迷宫剪支
// 打印剪支后的迷宫
printf("\n剪支后的迷宫:\n");
// 打印带正确路线的迷宫
printf("\n标记迷宫路线:\n");
}
这里我多加了一部分“打印剪支后的迷宫”,为了让大家可以看到中间过程,方便调试。
4. 打印迷宫
这就是一个普通的二维数组打印,代码如下:
void PrintMaze(int arrMaze[][MAX_SIZE])
{
int i, j;
for (i = 0; i < MAX_SIZE; i++)
{
for (j = 0; j < MAX_SIZE; j++)
{
printf("%3d", arrMaze[i][j]);
}
printf("\n");
}
}
5. 迷宫剪支
5.1 空间复制
由于我们做剪支时会修改二维数组的内容,为了保持原始数组不被破坏,我们要先复制出一个新的二维数组。复制函数如下:
void Copy(int* pDest, int* pSrc, int cnt)
{
while (cnt--)
{
*pDest++ = *pSrc++;
}
}
这几乎是课本上的例子程序,应该不用多介绍了。没学过指针的同学可以用数组的方法来实现。这里又涉及到二维数组的空间当一维数组来使用。
接下来,我们就可以在一块复制出来的迷宫里做任何想要的操作了。
5.2 剪支
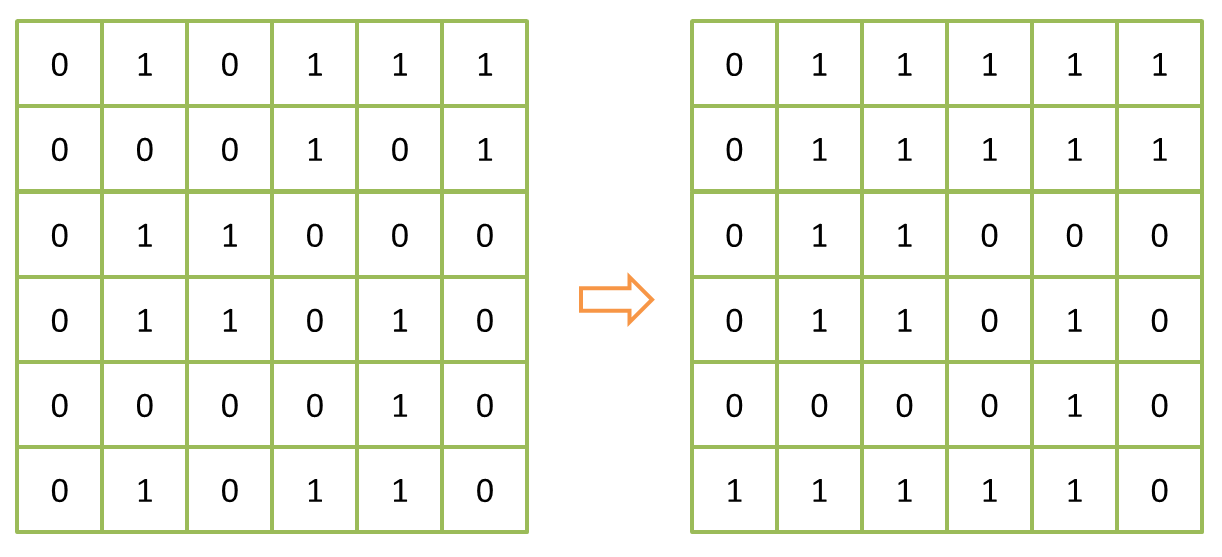
如图所示,我们的目标就是把左边这个二维数组转换成右边这个二维数组。
算法很简单,遍历二维数组,找到上下左右四个位置中只有一个或根本没有0的位置,如果它是0则改为1。
用人话说就是找到每条死路的最后一个位置,把它变成1。这样循环下去就能够将整条死路彻底封死。如下图:
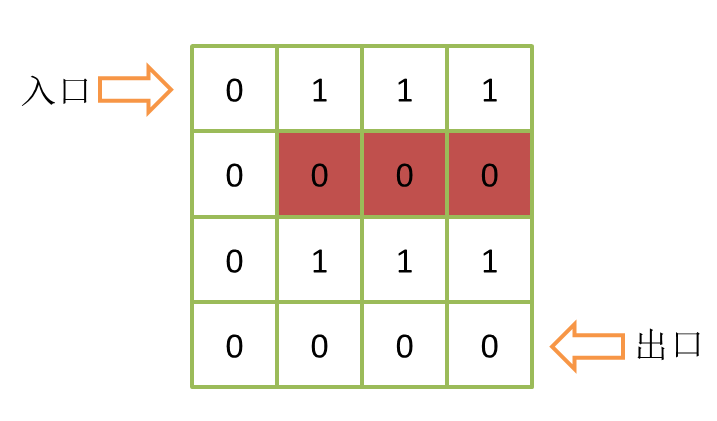
图中红色部分是一条死路,但我们遍历一遍只能把最右边的红色位置写入1,此时死路的尽头变成了中间这个红色方块。我们还需要继续循环,但这种死路有几个长度就循环几次的方式显然不是最优解。因此我们要设计一个算法能够一次就封死整个路径。
代码如下:
int CountPath(int maze[][MAX_SIZE], int i, int j)
{
int cnt = 0;
// Up Point
if (i > 0)
{
if (maze[i - 1][j] == 0 || maze[i - 1][j] == 2)
{
cnt++;
}
}
// Down Point
if (i < MAX_SIZE - 1)
{
if (maze[i + 1][j] == 0 || maze[i + 1][j] == 2)
{
cnt++;
}
}
// Left Point
if (j > 0)
{
if (maze[i][j - 1] == 0 || maze[i][j - 1] == 2)
{
cnt++;
}
}
// Right Point
if (j < MAX_SIZE - 1)
{
if (maze[i][j + 1] == 0 || maze[i][j + 1] == 2)
{
cnt++;
}
}
return cnt;
}
void FindNext(int maze[][MAX_SIZE], int i, int j)
{
int cnt;
int line, colum;
// Up Point
if (i > 0)
{
line = i - 1;
colum = j;
if (maze[line][colum] == 0)
{
if (CountPath(maze, line, colum) == 1)
{
maze[line][colum] = 1;
FindNext(maze, line, colum);
}
}
}
// Down Point
if (i < MAX_SIZE - 1)
{
line = i + 1;
colum = j;
if (maze[line][colum] == 0)
{
if (CountPath(maze, line, colum) == 1)
{
maze[line][colum] = 1;
FindNext(maze, line, colum);
}
}
}
// Left Point
if (j > 0)
{
line = i;
colum = j - 1;
if (maze[line][colum] == 0)
{
if (CountPath(maze, line, colum) == 1)
{
maze[line][colum] = 1;
FindNext(maze, line, colum);
}
}
}
// Right Point
if (j < MAX_SIZE - 1)
{
line = i;
colum = j + 1;
if (maze[line][colum] == 0)
{
if (CountPath(maze, line, colum) == 1)
{
maze[line][colum] = 1;
FindNext(maze, line, colum);
}
}
}
}
void CutBranch(int arrMaze[][MAX_SIZE])
{
int i, j;
arrMaze[0][0] = 2; // entry
arrMaze[MAX_SIZE - 1][MAX_SIZE - 1] = 2; // exit
for (i = 0; i < MAX_SIZE; i++)
{
for (j = 0; j < MAX_SIZE; j++)
{
if (arrMaze[i][j] != 0)
{
continue;
}
if (CountPath(arrMaze, i, j) <= 1)
{
arrMaze[i][j] = 1;
FindNext(arrMaze, i, j);
}
}
}
}
我们通过调用CutBranch()函数来遍历每一个位置。注意,这里只做了一次遍历。
当某个位置是0时,调用CountPath()函数计算出它的周围有几个0。如果是0个或1个,说明它是死路,修改它的值为1之后再调用FindNext()函数判断它周围的位置。
重点说一下,FindNext()函数,它的参数是一个二维数组和一组i,j表示的位置。功能是判断这个位置上下左右四个位置是否为死路,如果是就修改成1之后再调用FindNext()寻找修改之后它周围是否存在死路的情况。
注意:
- 在FindNext()中首先要判断是否在迷宫边上,否则直接访问可能会造成数组越界
- 由于入口和出口两个位置也满足死路的条件,因此我们在CutBranch()中把它们置为2
CutBranch()函数执行完后,我们就得到了一个只有一条正确路线的迷宫。
6. 标记路线
最后,把我们得到这条路径在原迷宫中标记出来。我们用9表示正确的路线。
void MarkMaze(int srcMaze[][MAX_SIZE], int markMaze[][MAX_SIZE])
{
int i, j;
for (i = 0; i < MAX_SIZE; i++)
{
for (j = 0; j < MAX_SIZE; j++)
{
if (markMaze[i][j] == 0)
{
srcMaze[i][j] = 9;
}
}
}
}
遍历markMaze,发现0就在srcMaze相应的位置上写9。
最后我们看看main函数中的函数调用:
void main()
{
int i, j, k;
int maze[MAX_SIZE][MAX_SIZE] =
{
{ 0, 1, 0, 1, 1, 1 },
{ 0, 0, 0, 1, 0, 1 },
{ 0, 1, 1, 0, 0, 0 },
{ 0, 1, 1, 0, 1, 0 },
{ 0, 0, 0, 0, 1, 0 },
{ 0, 1, 1, 1, 1, 0 }
};
int mazeCpy[MAX_SIZE][MAX_SIZE];
// 打印原始迷宫
printf("原始迷宫:\n");
PrintMaze(maze);
// 迷宫剪支
Copy((int*)mazeCpy, (int*)maze, MAX_SIZE * MAX_SIZE);
CutBranch(mazeCpy);
// 打印剪支后的迷宫
printf("\n剪支后的迷宫:\n");
PrintMaze(mazeCpy);
// 打印带正确路线的迷宫
MarkMaze(maze, mazeCpy);
printf("\n标记迷宫路线:\n");
PrintMaze(maze);
}
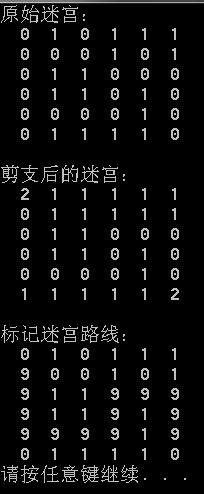
看看最后的执行结果:
7. 总结
这个算法是不是没有用到任何大家没学过的知识呢。先把我当代码看懂,之后考虑下面两个问题:
- 这个算法找到的路线是否一定是最短的路线呢?
- 判断每个位置是否在迷宫边上非常麻烦,有没有什么好办法简化这个操作呢?
请大家仔细思考这两个问题,我会在群里公布优化后的代码。
8. 课后作业

把一个硬币抛5次,打印出所有可能出现的情况。1表示正面,0表示背面。比如:
全正面
1 1 1 1 1
全背面
0 0 0 0 0
我是天花板,让我们一起在软件开发中自我迭代。
如有任何问题,欢迎与我联系。