评估假设
我们之前已经学习过一些机器学习的算法,现在我们来谈谈如何评估算法学习得到的假设。当发现预测的结果和实际的数据有误差的时候,我们需要进行一些调整来保证预测的准确性,大部分情况下,有以下几种办法来调整假设函数:
- 获取更多的训练集
- 减少特征的数量
- 尝试使用更多的特征
- 尝试使用多项式特征
- 增大或减小lambda
假设函数相对于训练集可能得到的误差很小,比如在过拟合的情况下,这时候就不能肯定假设函数是准确的。因此,我们有时候将数据集分成两块:训练集和测试集,一般来说训练集占70%,测试集30%。定义训练集的误差为,测试集为
。这样,我们要做的就是:通过训练集训练来最小化
和计算测试集
的误差。
对于线性回归:
对于分类问题:
当或
时,
;否则,
。
他们对于测试集的平均误差为:
这个给与我们测试集中错误分类的比例。
模型选择-训练集、验证集、测试集
由于学习算法可能对于训练集的数据相对很吻合,但不代表这是一个好的假设,之前说过了,这可能是过拟合的情况,从而导致预测的结果在测试集中的表现会不尽如人意。从当前数据集训练出的假设函数的误差是会比其他数据集要小的。
提供多个不同级数的多项式模型时,我们可以使用系统的方法来鉴别是否是最好的函数。为了选择最佳的假设,可以对于每一个不同的级数的多项式进行计算,得出他们的误差,从而比较出哪一个才是最合适的。
上文中我们将数据集分成了训练集和测试集两部分,实际情况中经常会分为三部分,其中60%为训练集,20%为交叉验证集,20%为测试集。我们可以分别计算这三部分的误差,

接下来:
- 通过训练集来针对每一个级数的多项式来最优化参数theta
- 通过交叉验证集来找到最误差最小的级数d
- 使用
来估计使用测试集得到的模型的泛化误差,这样的话,多项式的级数就不用通过测试集训练得到了。
诊断偏差与方差
当运行一个学习算法时,若这个算法的结果不理想,多半是出现两种情况:要么是偏差比较大(high bias),要么是方差比较大(high variance)。换句话说,要么是欠拟合问题要么是过拟合问题。
即高偏差导致欠拟合,高方差导致过拟合。理想情况下,我们要在这两者之间找到最佳的平均值。
当增加多项式的级数d时,训练集的误差将会减小。同时当增加级数d到达某个点时,交叉验证误差会渐渐的减小,然后其会伴随着d的增加而增加,图像为一个凸曲线。如下图:

总的来说:

正则化和偏差、方差
在之前的课程中已经学习过通过正则化来解决过拟合问题,现在再来谈谈正则化和偏差方差之间的关系。

在上图中,当很大,对于
,
..的惩罚都很大,则假设函数将会等于或近似于
,最终得到的假设函数就是一条直线,因此这个假设对于数据严重欠拟合。另一个情况当
很小时,趋向于0,那么正则化项趋向于0,得到的假设函数则会出现过拟合的情况。只有当我们取一个比较合适的
时,我们才能得到对数据拟合比较合理的
的值。
那么如何选择合适的模型和合适的正则化参数呢,具体有如下几个步骤:
1. Create a list of lambdas (i.e. λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24});
2. Create a set of models with different degrees or any other variants.
3. Iterate through the λs and for each λ go through all the models to learn some \ThetaΘ.
4. Compute the cross validation error using the learned Θ (computed with λ) on the J_CV (Θ) without regularization or λ = 0.
5. Select the best combo that produces the lowest error on the cross validation set.
Using the best combo Θ and λ, apply it on J_test (Θ) to see if it has a good generalization of the problem.
将的取值和
的曲线画出来如下所示:

随着
值的增加而增加,因为
的值增大会对应着高偏差问题,此时连训练集都不能很好的拟合,当
很小时,对应着你可以很容易地用高次多项式拟合你的数据。对于交叉验证的误差,如图中粉色的图像所示,当
很大时,会出现欠拟合问题,因此是那一片是高偏差区域,此时交叉验证集的误差会很大,当
很小时,会出现过拟合问题,对应的是高方差问题,因此交叉验证集的误差也会很大。同样的,总会有中间的某个点对应的
表现的结果正好合适,交叉验证误差和测试误差都很小。
学习曲线
当训练集很小的情况下,比如只有两三条数据的时候,我们很容易训练一个二次的算法来拟合数据,并且算法的误差可能几乎为0,因此,
- 当训练集增大时,二次函数的误差将会增加
- 随着集合数据的增加,最终的误差会渐渐趋向于平稳
具体变化如下图所示:
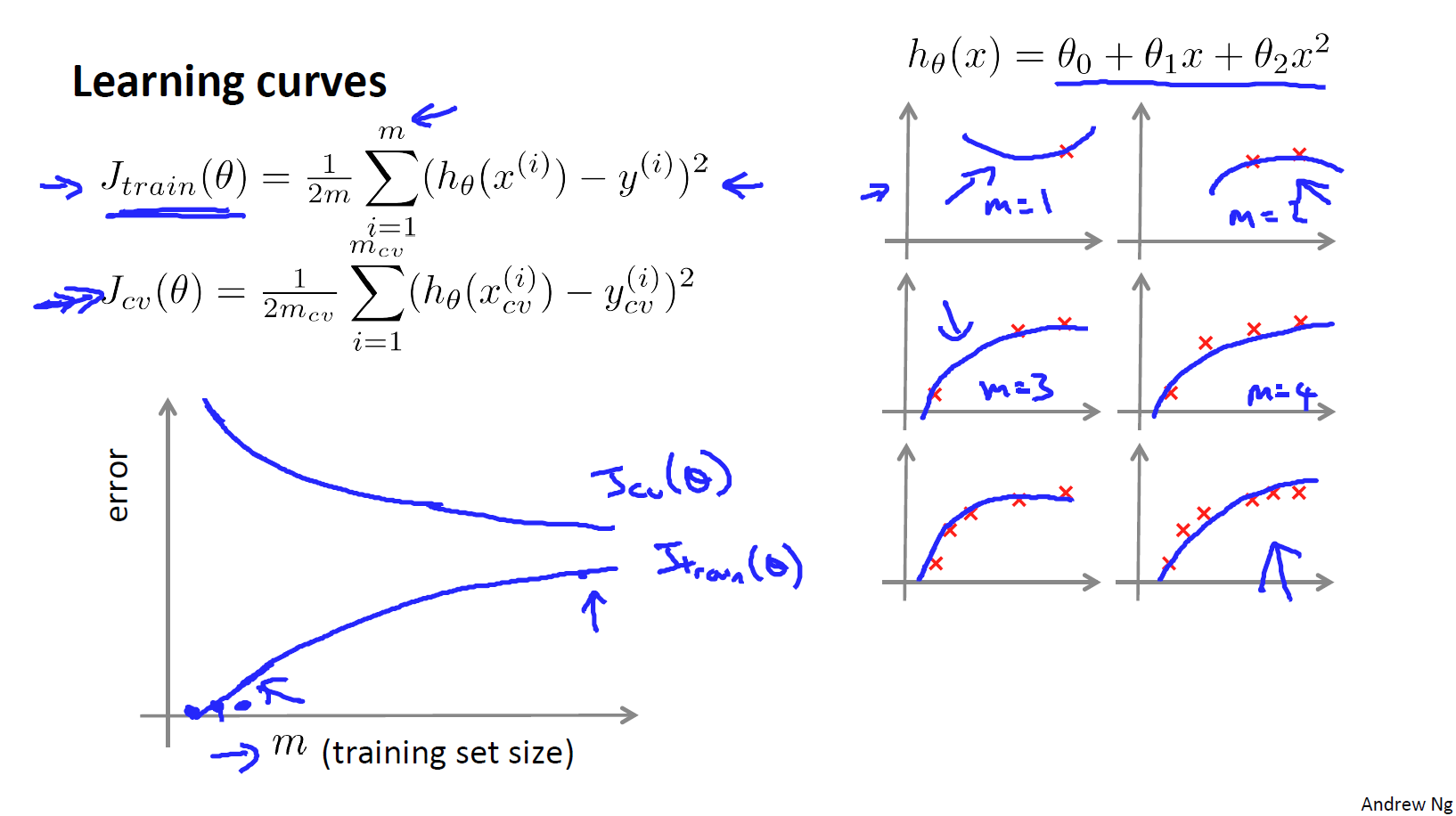
随着训练集的增加,交叉验证集的误差将会慢慢减小知道趋向于某一个值,因为拟合数据越多,就越能拟合出合适的假设。
那么如果出现了高偏差的情况,学习曲线会变成什么样子:
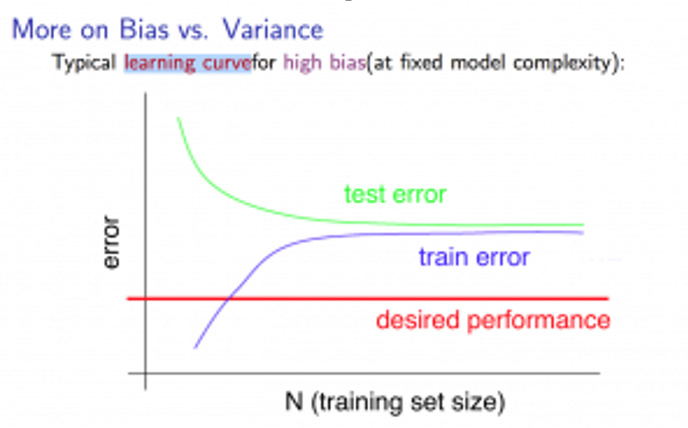
若训练集量比较小,那么拟合效果当然不好,导致交叉验证集的误差会很大,那么随着训练集的增加,拟合效果渐渐的变好了,交叉验证集的误差也会渐渐变小,当训练集增大到某一个量时,我们可能就会找到一条最有可能拟合数据的直线,并且此时即便继续增加训练集的样本容量,还是会得到一条差不多的结果。那么对于训练误差,一开始也是很小的,但在高偏差的情况下,训练集的误差会逐渐增大直到最后接近交叉验证误差,这是因为你的参数很小,但又有很多数据,当m很大时,训练集和交叉验证集的误差将会非常接近。总的来说能得出一个结论,如果一个算法有高偏差,那么选用更多的训练集数据并不能很好的改善算法。
对于高方差的情况,如下图:

一开始训练集的误差是很小的,但随着训练集容量的增加,误差会渐渐变大,也就是说数据越多,就越难将训练集数据拟合的很好,但总的来说,训练集的误差还是很小。那么对于交叉验证集,由于是高方差的情况,误差会一直都很大,虽然也会慢慢减小,但在训练误差和交叉验证误差之间依然有一段很大的差距。总的来说得出的结论就是,如果我们考虑增加训练集样本的容量,对于改善算法还是有一定的帮助的,因为很显然交叉验证误差再慢慢减小,那么测试集的误差也会慢慢减小,当然同样这个也能告诉我们这个算法可能存在高方差的问题。
总结
上文中一开始我们有说过几种不同的方法来改善假设函数,但往往有些人只是凭借自己的感觉来决定使用哪种方法,那么通过本文介绍的一些知识,我们可以得出,这几种方法分别对应于解决什么问题:
- 获取更多的训练集 --> 解决高方差问题
- 减少特征的数量 --> 解决高方差问题
- 尝试使用更多的特征 --> 解决高偏差问题
- 尝试使用多项式特征 --> 解决高偏差问题
- 增大lambda --> 解决高方差问题
- 减小lambda --> 解决高偏差问题
那么这里再补充一下对于神经网络的诊断:
- 一个相对简单的神经网络模型,隐含单元比较少或者隐藏层很少时,那么拟合时选择的参数就会比较小,容易出现欠拟合,但他的优势
- 拟合一个复杂的神经网络模型时,那么其参数一般比较多,容易出现过拟合,这种结构的计算量相对会很大。但过拟合问题可以使用正则化来进行修正。通常使用大型网络模型然后使用正则化来防止过拟合问题相对于使用简单的神经网络拟合的效果要更好。
总的来说,模型的复杂程度的影响有以下几点:
- 低阶多项式,也就是低复杂程度的模型有高偏差和低方差的问题,这种情况下,模型的拟合程度较差
- 高阶多项式,也就是高复杂程度的模型对于训练集的拟合效果相对较好,但对于测试集的拟合效果非常差,会出现低偏差和高方差问题。
- 在现实中,我们需要在两者之间选择一个合适的模型,使其能很好的来拟合数据。
以上,为吴恩达机器学习第六周Advice for Applying Machine Learning部分的笔记。