黄金分割的核心,就是边的总长a+b和长边a的比例,与a比b的比例相等。和黄金分割有关的任何变形,都和这个核心紧密相关。如下图的数学式子所示。我们假设这个比例是Φ
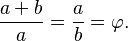
有了上面的式子我们就可以算出来Φ的值
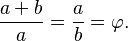

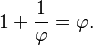
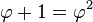
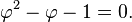

其中包含了无理数,所以在数学中是不容易计算的。但是在几何中却可以轻易的画出来。
随便画个正方形,找到随便一条边的中点,比如下图中的AB边的中点E,以EC为半径画弧,就形成了下图中的矩形,这就妥妥是一个黄金矩形了。注明一下,这个弧线和后面我要说的黄金螺旋没有半毛钱关系。辅助线画完就可以擦掉了。

把矩形扩展继续画下去就是下图中的黄金矩形。可以看到黄金矩形和正方形有着密不可分的联系,去掉以其短边为边长的正方形时,剩下的矩形仍然是黄金矩形。

把矩形标上数字,连接上圆滑的曲线,就是传说中的黄金螺旋了。图上的数字说明一下,最大的黄金矩形的长边设为Φ(约等于1.618),短边设为1。你就把以短边为边长的那个正方形,对,就是左边这个,全部都标上1,看得更清楚。右上角深灰色的这个正方形的长度就有了两种表示方法。Φ-1和1/Φ。前者很明显,后者如果不理解,请回到本文第一句话。还记得吗,长边和短边的比例是Φ。这是通过比例倒算出来的。有了这个比例,接下来的正方形的边长就都不是事儿了。如图表示。

这尼玛数字这么复杂,你是不是在坑我。好吧,接下来说个黄金螺旋的简化版。下图是根据一个数列画出来的。分别是1, 1, 2, 3, 5, 8, 13, 21, 和 34,分别是从小到大各个正方形的边长。这个数列有个特高大上的名字,叫斐波那契数列,这个螺旋叫斐波那契螺旋。这个数列的特别之处在于,后面一个数字除以前面的数字,结果会越来越接近Φ。比如34除以21约等于1.619.大概因为它好画,所以他的使用率比标准的黄金螺旋要高多了。


建筑,绘画,乃至自然界都有非常多的黄金分割存在。下面随便列出几个例子。


这个很有意思,嘴唇张开最好看的弧度,是门牙和旁边的牙齿的长度比例是黄金比例的时候~

