概念
- 实数与数轴
- 实数:有理数与无理数
- 实数性质:1) 有序性 2)完备性
- 实数集
- 所有实数构成的集合;
- 区间:开区间(a,b)、 闭区间[a,b]、半开半闭区间 [a,b) (a,b];
- 邻域:称开区间( x0 -a , x0 +a )为x0点的a 邻域.
自然数-N, 整数-Z, 实数-R, 有理数-Q
-
函数
设集合
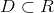
设在某一问题中,存在两个变量x, y , 如果对于变量x所取的每一个值x, 通过一定规律(关系),都有唯一变量y与之对应,此时称变量x为自变 量,变量y叫做因变量,又叫做x的函数,记为y =f ( x ). 三个要素: 自变量x, 函数关系f, 因变量y 基本初等函数:
反,对,幂,三,指;
- 反函数: 与原来函数关于y=x对称,对于每一个自变量x都有
唯一一个y对应,则称该函数存在反函数; - 对数函数: 定义域是 X>0;
- 指数函数: 与对数函数互为反函数,定义域为全体实数R;

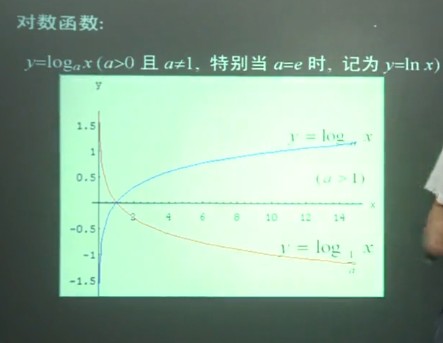
- 幂函数:
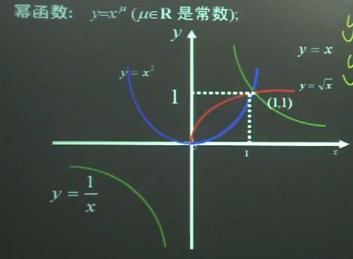
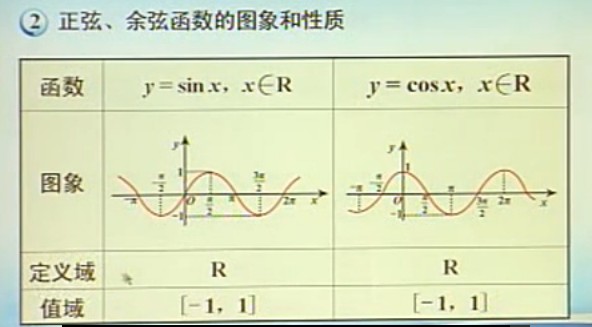
- 三角函数:

- 上图 1,每个相对顶点互为倒数; 2, 每一个白色的倒三角的平方和等于下边顶点的平方 ;
<img src="https://raw.githubusercontent.com/liangxifeng833/my_program/master/images/math/math-sanjiao-function-1.jpg" width="700" />


<img src="https://raw.githubusercontent.com/liangxifeng833/my_program/master/images/math/math-sanjiao-function-5.jpg" width="700" />
- 复合函数:要求主函数的定义域∩子函数的值域≠空;
- 初等函数:基本初等函数通过四则运算后得到的表达式;