Copy from BYVoid
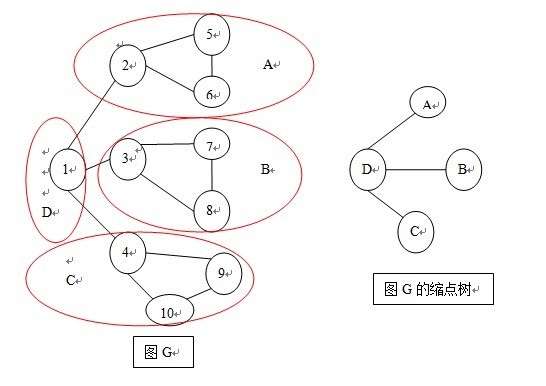
一个有桥的连通图，如何把它通过加边变成边双连通图？方法为首先求出所有的桥，然后删除这些桥边，剩下的每个连通块都是一个双连通子图。把每个双连通子图收缩为一个顶点，再把桥边加回来，最后的这个图一定是一棵树，边连通度为1。

统计出树中度为1的节点的个数，即为叶节点的个数，记为leaf。则至少在树上添加(leaf+1)/2条边，就能使树达到边二连通，所以至少添加的边数就是(leaf+1)/2。具体方法为，首先把两个最近公共祖先最远的两个叶节点之间连接一条边，这样可以把这两个点到祖先的路径上所有点收缩到一起，因为一个形成的环一定是双连通的。然后再找两个最近公共祖先最远的两个叶节点，这样一对一对找完，恰好是(leaf+1)/2次，把所有点收缩到了一起。

A - Road Construction
一个不错的博客

     #include<cstdio>
     #include<stack>
     #include<cstring>
     using namespace std;
     const int MAXN=1010;
     const int MAXE=2010;
     struct Node
     {
         int to,next;
         bool cut;
     };
     Node edge[MAXE];
     int head[MAXN];
     int low[MAXN],dfn[MAXN],onStack[MAXN];
     int cnt,clocks;
     stack<int> sta;
     int belong[MAXN];
     int degree[MAXN];
     int blocks;
     void addEdge(int u,int v)
     {
         edge[cnt].to=v;
         edge[cnt].next=head[u];
         edge[cnt].cut=false;
         head[u]=cnt++;
     }
     void DFS(int u,int fa)
     {
        low[u]=dfn[u]=++clocks;
        onStack[u]=1;
        sta.push(u);
        for(int i=head[u];i!=-1;i=edge[i].next)
        {
            int v=edge[i].to;
            if(v==fa) continue;
            if(dfn[v]==0)
            {
                DFS(v,u);
                low[u]=min(low[u],low[v]);
                if(low[v]>dfn[u])
                {
                    edge[i].cut=true;
                    edge[i^1].cut=true;
                }
            }
            else if(onStack[v]&&dfn[v]<dfn[u])
            {
                low[u]=min(low[u],dfn[v]);
            }
        }
        if(dfn[u]==low[u])
        {
            blocks++;
            while(true)
            {
                int curr=sta.top();
                sta.pop();
                onStack[curr]=0;
                belong[curr]=blocks;
                if(curr==u) break;
            }
        }
     }
     void work(int n)
     {
         memset(dfn,0,sizeof(dfn));
         memset(onStack,0,sizeof(onStack));
         clocks=0;
         while(!sta.empty()) sta.pop();
         memset(belong,0,sizeof(belong));
         memset(degree,0,sizeof(degree));
         blocks=0;
         for(int i=1;i<=n;i++)
         {
             if(dfn[i]==0)
             {
                 DFS(i,-1);
             }
         }
         for(int i=1;i<=n;i++)
         {
             for(int j=head[i];j!=-1;j=edge[j].next)
             {
                 if(edge[j].cut)
                 {
                     degree[belong[i]]++;
                 }
             }
         }
         int ans=0;
         for(int i=1;i<=blocks;i++)
         {
             if(degree[i]==1)
             {
                 ans++;
             }
         }
         printf("%d\n",(ans+1)/2);
     }
     int main()
     {
         int n,m,a,b;
         while(scanf("%d%d",&n,&m)!=EOF)
         {
             memset(head,-1,sizeof(head));
             cnt=0;
             for(int i=0;i<m;i++)
             {
                 scanf("%d%d",&a,&b);
                 addEdge(a,b);
                 addEdge(b,a);
             }
             work(n);
         }
     }