本系列文章记录学习的过程。
0. 前言
由于课程授课和课件(Lecture Slides)均为英文,所以文中许多专有名词会标注英文,中文翻译参考《Algorithms Fourth Edition》中文版。课件以及其它资料下载链接会在文末给出。
1. 动态连通性(Dynamic Connectivity)
1.1 定义
什么是动态连通性?
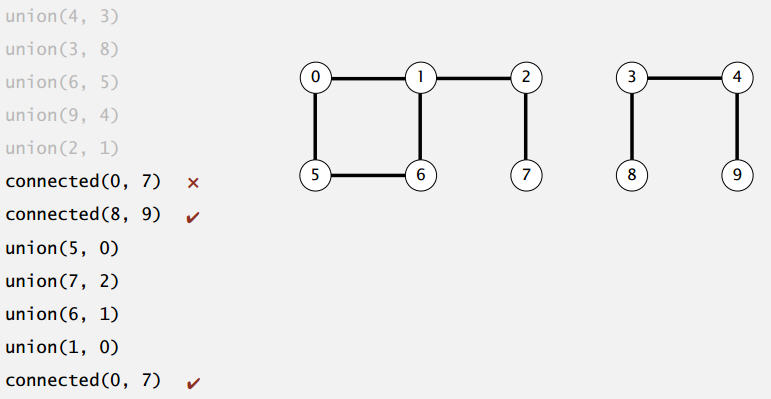
Given a set of N objects.
・Union command: connect two objects.
・Find/connected query: is there a path connecting the two objects?
给定几个数的集合
- Union操作: 在两个数之间加一条连接。
- Find/connected查询: 判断两个数之间是否有连接。
1.2 建立模型
如何选择具体的数据结构模型呢?
动态连通性的应用十分广泛:
- 照片的像素
- 网络中的电脑
- 社交网络中的两个人
- 电路芯片中的晶体管
- 数学集合中的元素
...
比较容易实现的选择:使用数组,让数组的每个下标代表每个数。
我们继续假设: “相连(is connected to)” 是两个数之间的一种关系,且这种关系满足以下条件:
- 自反性(Reflexive): p和p是相连的;
- 对称性(Symmetric): 如果p和q是相连的,那么q和p也是相连的;
- 传递性(Transitive): 如果p和q相连且q和r相连,那么p和r相连。
当两个数相连时,它们属于同一个等价类(Connected Components)。
等价类,就是所有相连的数的集合,这个集合必须包含所有相连的数。
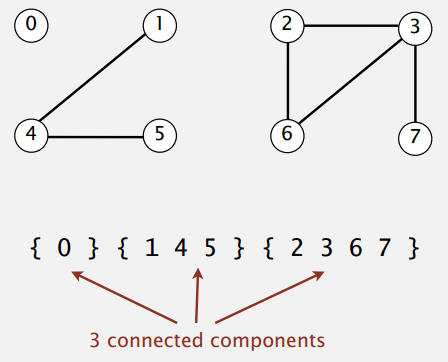
具体的操作,给定两个数:
- Find操作: 查看两个数是否属于同一个等价类。
- Union操作: 将两个数连接起来,这个操作其实就是将两个数所在的等价类联合成一个等价类。
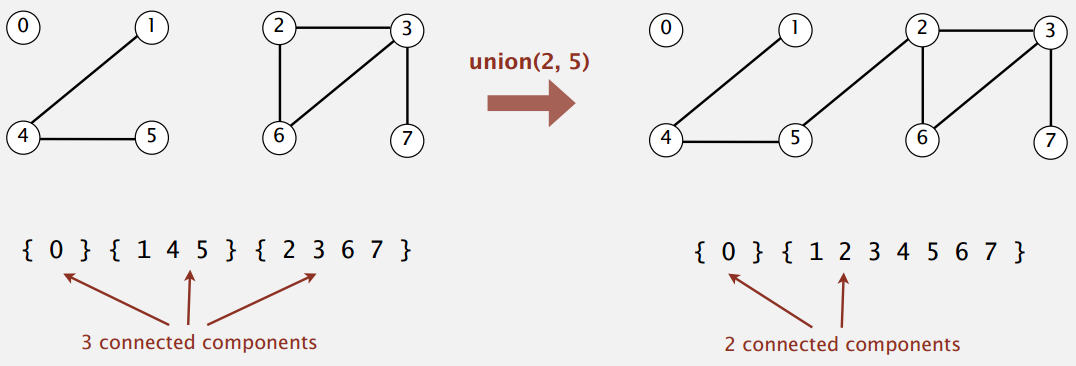
在这里约定一下使用的术语:
| 英文 | 汉语术语 |
|---|---|
| Connected Components | 等价类 / 分量 |
| node | 节点 |
1.3 Union-Find数据类型(Union-Find data type)
由1.2 我们得出了简单的数据模型,现在需要设计具体的数据类型,我们的目标是:
- 为Union-Find操作设计出一个高效的数据类型
- 每个数据类型包含N个数,N可能会很大
- 操作的次数M可能很大
- Find操作和Union操作可能会交叉进行
以下是API:
| public class UF | |
|---|---|
| UF(int N) | 用整数N(0到N-1)初始化N个点 |
| void union(int p, int q) | 为点p和点q之间添加一条连接 |
| boolean connected(int p, int q) | 判断点p和点q是否属于同一个分量 |
| int find(int p) | p所在分量的标识符(0到N-1) |
| int count() | 分量的数量 |
2. Quick Find算法
2.1 数据结构
- 整数型数组id[],长度为N。
- p和q是相连的等价于数组中p下标和q下标的数相同。
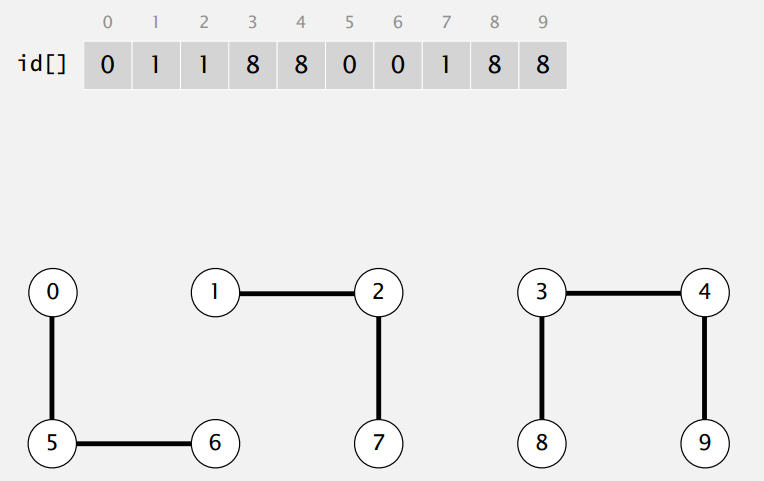
2.2 Java实现

2.3 算法分析
QuickFind算法太慢了。
下表是最坏情况下QuickFind算法对一组点操作使用的时间消耗。
| 算法 | 初始化 | union操作 | find操作 |
|---|---|---|---|
| QuickFind | N | N | 1 |
Union操作过于缓慢:如果要对N对点进行union操作,最多需要对数组访问N^2次。
3. Quick Union算法
3.1 数据结构
- 整数型数组id[],长度为N。
- id[i]中存储i的父节点( 也就是形成一个链接,直到其父节点就是它自己,说明到头了)
- i的根节点(root)是id[id[id[id[...id[i]...]]]]
具体操作:
- Find操作:检查p和q是否拥有同一个根节点 。
-
Union操作: 为了合并p和q各自所在的分量,将p的根节点改为q的根节点。
 QuickUnion
QuickUnion
3.2 Java实现

3.3 算法分析
对一对点进行操作需要访问数组的次数,图中是最坏情况。
| 算法 | 初始化 | union操作 | find操作 |
|---|---|---|---|
| QuickFind | N | N | 1 |
| QuickUnion | N | N* | N |
*:包括了寻找根节点的操作。
QuickFind的缺点
- Union操作太慢了,最差为N
- 树是平的,但是维护这个状态时间耗费太大了
QuickUnion的缺点
- 树可能会很高
- Find操作太慢了,最差为N
4. 改进1 - 加权(weighting)
4.1 数据结构
加权QuickUnion(Weighted QuickUnion)
- 改进QuickUnion,避免太高的树
- 对每个树的大小(包含点的数量)进行记录
- union操作时,比较两个点所在树的大小,小数的根节点连接到大树的根节点之上

数据结构其实和QuickUnion相同,但是需要再维护一个额外的数组sz[i],用来记录以i节点为根节点的分量的大小(及分量中数的多少)
4.2 Java实现
Find操作:和QuickUnion相同
return root(p) == root(q);
Union操作:改进的QuickUnion
- 将较小的树的根节点连接到大的树的根节点上
- 不断更新sz[]数组
int i = root(p);
int j = root (q);
if(i == j) return;
if(sz[i] < sz[j]) { id[i] = j; sz[j] += sz[i];}
else { id[j] = i; sz[i] += sz[j];}
4.3 算法分析
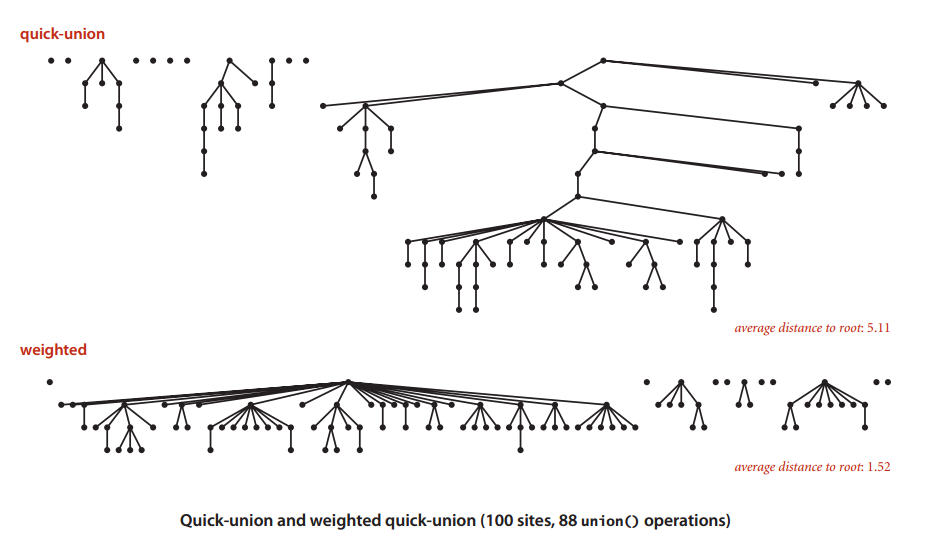
运行时间
- Find操作: 时间和p以及q的深度成正比
- Union操作: 给定根节点,时间为常数
命题: 任意节点x,其深度最大为lg N 。
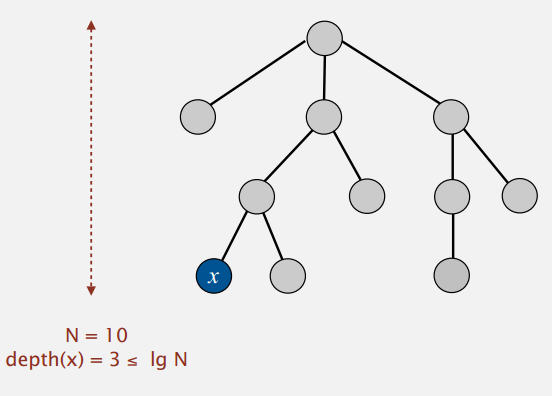
证明:
什么时候x的深度会增大呢?
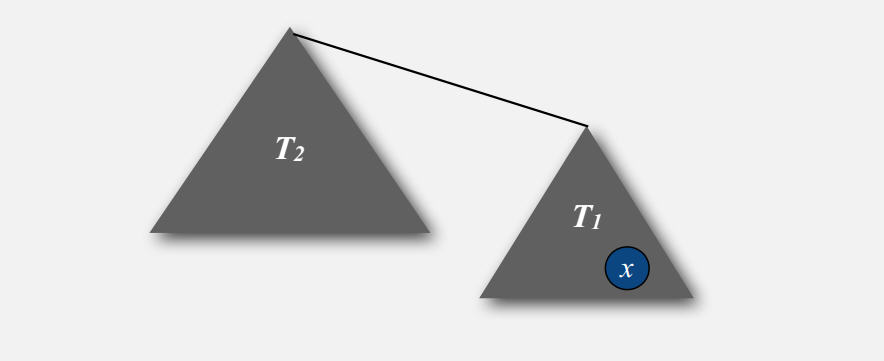
当树T2比树T1大,即|T2| >= |T1|时,包含x的树T1成为另一个树T2的子树时,x的深度会加1。由此推出:
- T1和T2合起来的新树,其大小至少是之前T1的2倍。(也就是x所在的树大小增大1倍,x的深度加1)
-
包含x的树最多可以翻倍lg N 次。
 WeightedQuickUnionAnalysis
WeightedQuickUnionAnalysis
算法分析
| 算法 | 初始化 | union操作 | find操作 |
|---|---|---|---|
| QuickFind | N | N | 1 |
| QuickUnion | N | N* | N |
| weighted QU | N | (lg N)* | lg N |
*:包括了寻找根节点的操作。
还可以优化吗?答案是肯定的。
5. 改进2 - 路径压缩(Path Compression)
5.1 数据结构
在计算点p的根节点root之后,每个经过的节点,如果其根节点不为root的话,让其根节点变成root,如图是带路径压缩的QuickUnion算法(Quick Union with Path Compression),下图是具体的过程。

5.2 Java实现
private int root(int i) {
int temp; // 临时节点
while(i != id[i]) {
temp = id[i]; // 用临时节点记录i节点的父节点
id[i] = find(i);// 将i节点的父节点置为根节点
i = temp; // 对i节点之前的父节点进行重复性判断
}
return i;
}
5.3 算法分析
使用带路径压缩的加权Quick Union算法,对于N个数,M次操作时,访问数组次数最多为c (N + M lg* N)。
(c为常数, lg* N是lg(lg(lg(...lg()...)))。)
对于N个数,M次操作时,有没有线性访问数组次数的算法呢?
- 理论上, WQUPC(Weighted Quick Union & Path Compression)不是线性的
- 实际中,WQUPC基本是线性的
现已证明,没有完全的线性算法存在。
6. 总结
使用带路径压缩的加权Quick Union算法,使得之前不可能被解决的问题现在可以被解决。

对于109次union操作和109次find操作:
- WQUPC让时间从30年变成了6s
- 超级计算机并不能帮助太多,但是好的算法可以让问题得到充分解决
7. 参考网址
[1] 课程首页(Course Page)
[2] Algorithms 4th
[3] 课件下载(Lecture Slides)