前言
模式匹配是数据结构需要解决的经典问题之一,由此衍生出许多算法。本文介绍模式匹配算法的复杂度从o(mn)逐步演化到o(m+n)的过程。
模式匹配
模式匹配描述了这样的一个问题:
字符串
T[1..n]和P[1..m]由字符集∑中的字符组成(m<=n),要求字符串T中和模式P所匹配的索引号。
朴素模式匹配算法
这个问题最简单的解决办法是:
从T的每一个字符
T[i]{1≤i≤n}开始依次向后比对P的每一个字符,如果全部匹配,则输出i;重复之前的操作,直到找到所有符合条件的i。
代码如下:
object KMPv1 {
def kmp(source:String,sequence: String):scala.collection.mutable.Seq[Int] = {
val sourceLen = source.length
val sequenceLen = sequence.length
if(sourceLen<sequenceLen)
return scala.collection.mutable.Seq.empty[Int]
var cursor = 0
val cursorMax = sourceLen-sequenceLen+1
var res:scala.collection.mutable.Seq[Int] = scala.collection.mutable.Seq[Int]()
while(cursor<cursorMax){//m-n+1
var isMatch = true
var cursorInner = 0
while(isMatch && cursorInner<sequenceLen){//m
isMatch = source.charAt(cursor+cursorInner) == sequence.charAt(cursorInner)
cursorInner+=1
}
if(isMatch){
res = res.:+(cursor)
}
cursor+=1
}
res
}
}
这个算法的复杂度是o(m*(n-m+1))=o(mn),它并没有利用到曾经匹配过的信息。
有限自动机的思想
有限自动机在接受到一个信号之后,会从一个状态转移到另外一种状态。
引入有限自动机的概念之后可以对模式匹配问题作如下变形:
将字符串
T[1..n]中的字符T[i]{1≤i≤n}依次输入有限自动机,自动机的状态q记录了信号输入之后与P[1..m]相匹配的字符数,当自动机的状态转移到m时我们接受此时的索引i-m为匹配索引。
举例来说:
假设P=ababaca由∑={a,b,c}中的字符组成,有限自动机的初始状态是0,在这个时候接受输入a则转移到状态1(因为输入a之后和P有一个匹配的字符);在状态为1的时候接受输入a则状态仍然是1,接受b则状态转移为2,接受c则状态转移为0(因为跟P没有匹配的字符)。
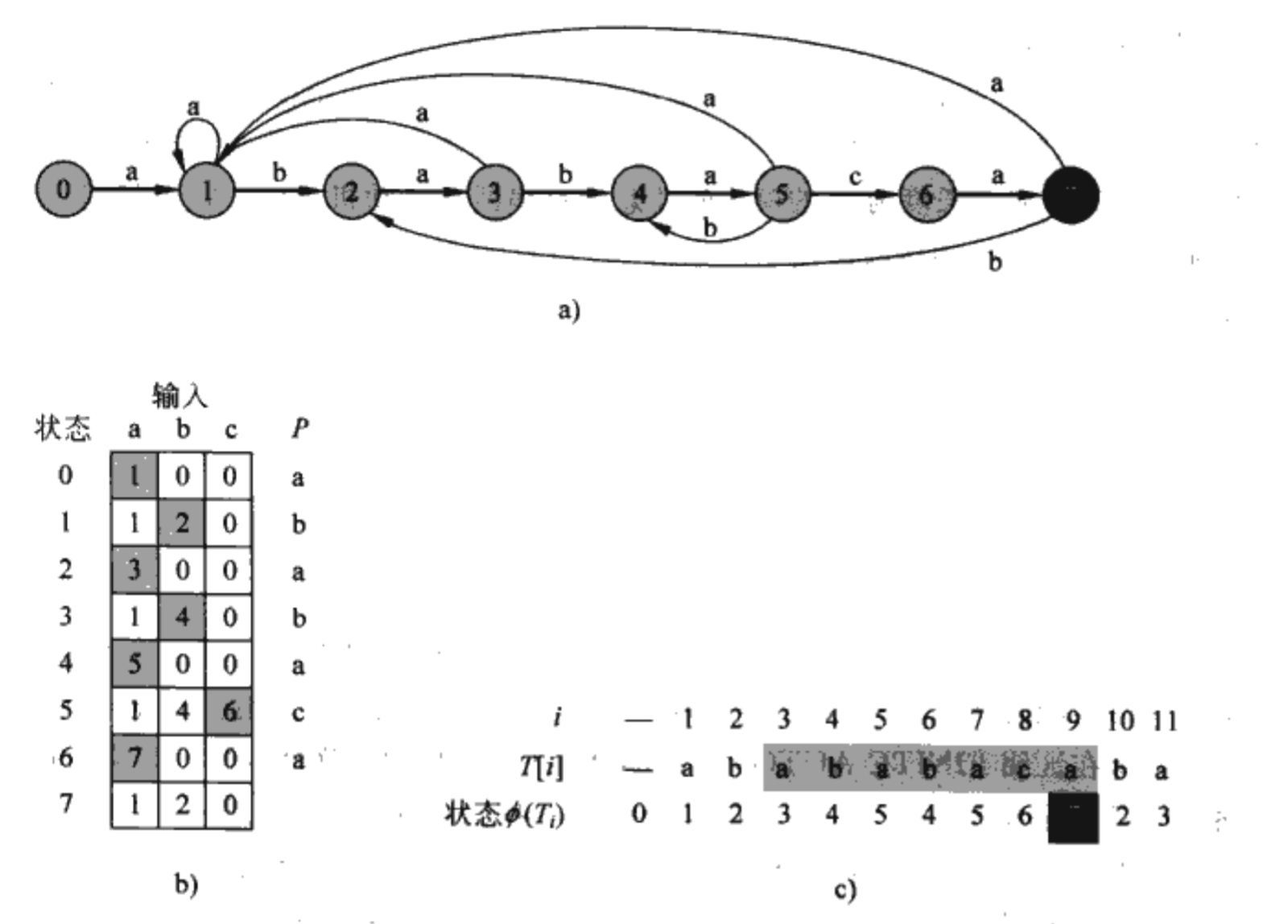
显然这个思想的关键在于构造出有限自动机的转移函数∂(q,signal)。从上图b可知,该函数只与m和|∑|(全集的字符个数)有关,该表共有(m+1)|∑|个状态值,计算每个状态值的复杂度最多是o(m^2),所以构造转移函数的复杂度最多达到o(|∑|m^3)。之后与T来匹配只需要o(n)的复杂度。整个算法的复杂度最多是o(n+|∑|m^3)。
此算法的复杂度远远大于朴素模式匹配算法的o(mn),但是它充分利用曾经匹配过的信息(存储在有限自动机的状态中),给了我们另外一种思路来思考这个问题,如果能将转移函数的复杂度优化到o(m),就可以大大降低整体的复杂度。
KMP算法
KMP算法在有限自动机的思想上做了一些调整,同样引入了状态这一概念,但是状态并不是由状态转移函数计算得到,而是通过前缀函数进行逻辑运算之后计算出来的。
举例来说:
如下图a,在输入T[9]=b之前,整个匹配过程处于状态q=5,即T[4..8]=P[0..4],此时输入T[9]=b,发现和P[5]=c不匹配,此时通过观察发现:
将
P向右移动2个位置刚好又有P[0..2]和T[6..8]匹配,此时状态是q=3。
输入T[9]=b之后发现匹配则状态变成q=4。
尝试将上述的观察过程理论化,发现因为P[0..4]的所有前缀中(除开P[0..4]本身),与T[4..8]的后缀所匹配的最大长度是31,所以尝试将P向右移动[当前状态q=5减去3等于2]个位置;又由于有T[4..8]=P[0..4],所以1处与T[4..8]作匹配等价于与P[0..4]作匹配。
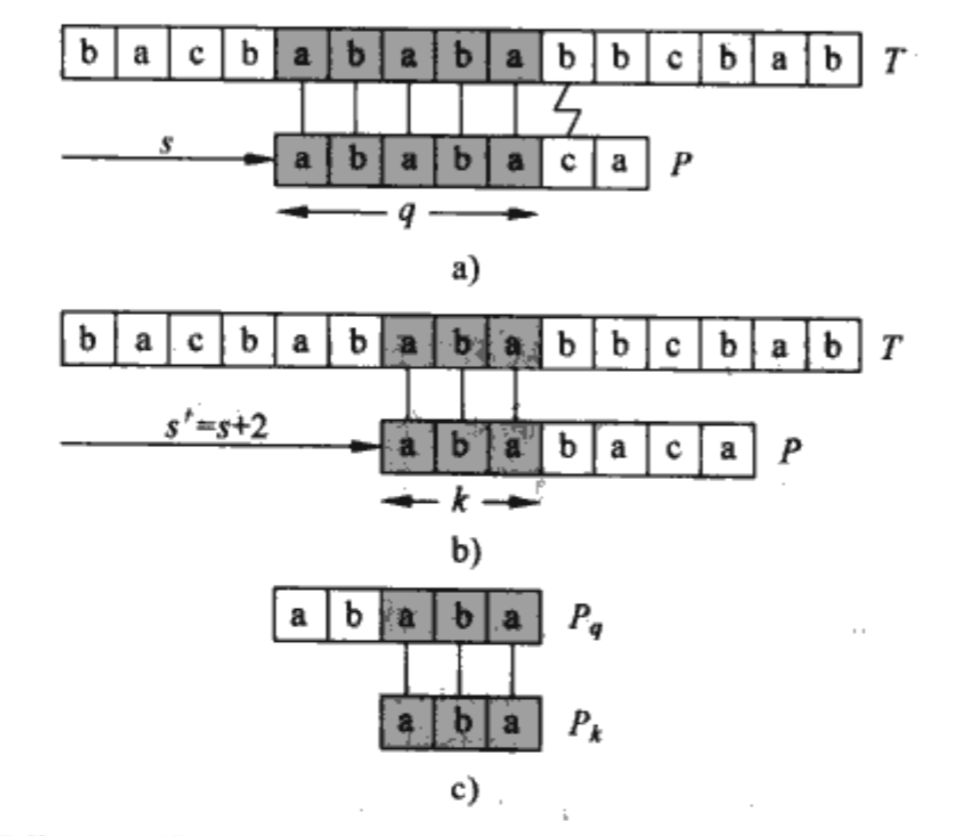
由此,下一个状态可以通过当前状态q和与P[1..q]的后缀匹配的最长前缀(除开自身)的函数来计算出。
计算前缀函数的伪代码如下:

匹配函数的伪代码如下:

scala实现如下:
/**
* Created by studyz on 17/3/16.
*/
object KMPv2 {
def kmpMatch(source:String, pattern: String):scala.collection.mutable.Seq[Int] = {
var res = scala.collection.mutable.Seq[Int]()
val statusArr = kmpPrefixFunc(pattern)
var k =0//表示已经匹配的个数
val n = source.length
val m = pattern.length
for(q <- 0 until n){//n次
while(k>0 && source.charAt(q) != pattern.charAt(k)){
k = statusArr(k-1)
}
if(source.charAt(q) == pattern.charAt(k)){
k+=1
}
if(k == m){
res = res.:+(q-m+1)
k = statusArr(k-1)
}
}
res
}
//pattern字符串第k位前缀的与自身匹配的最长后缀
//P[1..m],1≤q≤m,0≤k<q,求k使得P[1..k]是P[1..q]的最长后缀,kmpPrefixFunc(q)=k
def kmpPrefixFunc(pattern:String):Array[Int]={
val m = pattern.length
val res = new Array[Int](m)
res(0) = 0
var k = res(0)
for(q <- 1 until m){
while(k>0 && pattern.charAt(k) != pattern.charAt(q)){
k = res(k)
}
if(pattern.charAt(k) == pattern.charAt(q)){
k+=1
}
res(q) = k
}
res
}
}
使用平摊分析法可知此算法的复杂度是o(m+n),其中前缀函数kmpPrefixFunc的复杂度是o(m),匹配函数kmpMatch的复杂度是o(n)。(//TODO)
参考文献:
- 算法导论第三版