一、基本概念

注意： 一个树只有一个根节点
（1）节点的度（degree）
一个节点拥有子树数

（2）节点分类
根节点（root）
内部节点
叶节点（leaf）

image.png

（3）节点之间的关系
双亲（parent）
兄弟（sibling）：左兄弟、右兄弟
孩子（child）: 左孩子、右孩子

（4）路径（path）
从节点n1到nk的路径定义为节点n1,n2,..., nk的一个序列，使得1≤ i＜k，节点ni是n_(i+1)的父亲。
这个路径的长（length）为该路径上边的条数。

（5） 树与节点的深度（depth）和高度（height）
概念的定义参考：《Data Structure and Algorithm Analysis in C》

节点的深度（depth）

节点ni的深度为从根到ni的唯一路径的长。

节点的高度（height）

节点ni的高度为从ni到一片树叶的最长路径的长。

树的深度： 树最深的叶子的深度
树的高度： 树的根节点的高度

下图：
节点D的深度为2，高度为1
节点B的深度为1，高度为2
该树的深度为3，高度也为3

该图标注的树的深度为4，源自《大话数据结构》，不建议使用这个定义。

image.png

引申：
森林(Forest)是由m（m≥0）颗互不相交的树组成。对于非空树的每个非叶子节点而言，其子树的集合即为森林。

二、 二叉树

image.png

二叉树的特点
（1） 每个节点最多有2个子树
（2） 子树之间有左右次序，不可交换
（3） 如果一个节点只有一颗子树，那么要区分左子树还是右子树

二叉树的5种基本形态
（1）空二叉树（没有节点）
（2）有一个根节点的二叉树
（3）根节点只有左子树
（4）根节点只有右子树
（5）根节点既有左子树，又有右子树

应用：求只有3个节点的二叉树有多少种形态？

（1） 首先按层分类，有2类：深度为2的，深度为3的
（2）3个节点，深度为2的二叉树只有一种情况；深度为3的情况分4种： 中间节点可以左孩子或者右孩子，最后一个节点也是可以是左孩子或者右孩子

image.png

3. 完全二叉树

一颗具有n个节点的二叉树按层序编号，若其所有节点的编号与对应的满二叉树节点编号相同，则这颗二叉树是完全二叉树。
正例

image.png

反例

image.png

完全二叉树的特点
（1） 所有叶子节点一定集中在最下面两层（一般的完全二叉树）或最下面一层（特殊的完全二叉树——满二叉树）
（2）最下层的叶子一定集中在左部连续位置
（3）倒数第二层若有叶子节点，一定集中在右部连续位置
（4）如果节点度为1，则该节点只有左孩子，没有右孩子
（5）同样节点数的二叉树，完全二叉树的深度最小

二叉树的性质
（1） 第i层至多有2^(i-1)个节点（i≥1）
![](http://latex.codecogs.com/gif.latex?
2^0,21, ... , 2^{i-1}, ...
)
（2） 层数为k的二叉树，至多有2^k - 1个节点
![](http://latex.codecogs.com/gif.latex?
2^{k} -1 = 2⁰⁺²1+ ... + 2^{k-1}
)
（3）对任何一颗二叉树T，如其终端节点数为n0，度为2的节点数为n2，则n0 = n2 + 1

一颗树，除了度为0的终端节点（如FGHIJ）和度为2的节点（如ABCD）之外，就只有度为1的节点了，如下图的E节点。

不妨设度为1的节点个数为n1，则树T总的节点个数
n = n0 + n1 + n2

由于除了根节点外每个节点都有分支线指向它，所以分支线总数
l = n - 1

换个角度，每个节点的发出分支个数要么为0（度为0的节点），要么为1（度为1的节点），要么为2（度为2的节点），所以分支线总数
l = n1 + 2*n2

将第一个方程带入第二、三个方程，消掉n1，-1移到等式右边变为1，得
n0 = n2 + 1
即，叶子节点个数是度为2的节点数加1

image.png

（4） 具有n个节点的完全二叉树深度为
这里的深度采用《Data Structures and Algorithm in C》
![](http://latex.codecogs.com/gif.latex?
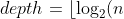depth = \lfloor\log_2(n)\rfloor \
layer = \lfloor\log_2(n)\rfloor + 1
)

度为k的完全二叉树的节点数n一定小于等于同样深度的满二叉树的节点数，一定大于深度比其小于1的满二叉树的节点数，即
![](http://latex.codecogs.com/gif.latex?
2^{k-1} - 1 < n \leqslant 2^k - 1
)
为了两边取对数，利用n是整数的性质，可以将上述不等式化为
![](http://latex.codecogs.com/gif.latex?
2^{k-1} \leqslant n < 2^k
)

对不等式两边取对数，
![](http://latex.codecogs.com/gif.latex?
k - 1 \leqslant \log_2(n) < k
)
所以，
![](http://latex.codecogs.com/gif.latex?
k = \lfloor\log_2(n)\rfloor + 1
)
（5）一个具有n个节点完全二叉树的节点从1按层序编号，对任一节点i（1 ≤ i ≤ n）有

若i > 1 ，则有双亲节点，编号为

![](http://latex.codecogs.com/gif.latex?
\lfloor\frac{n}{2}\rfloor
)

若2i ≤ n，则有左孩子节点，编号为

![](http://latex.codecogs.com/gif.latex?
2i
)

若2i+ 1 ≤ n，则有右孩子节点，编号为

![](http://latex.codecogs.com/gif.latex?
2i+1
)

参考资料：
《大话数据结构》
《Data Structures and Algorithm in C》